
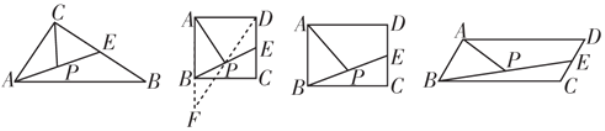
【题目】(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,则称CP是△ABC的“双中线”.若∠ACB=90°,AC=3,AB=5,则CP=________;
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”.若AB=4,则AP的长为__________;(按图示辅助线求解)
(3)在图3中,AP是矩形ABCD的“双中线”.若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(4)在图4中,AP是□ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°,求△ABP的周长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)AP的长为
;(3)AP的长为![]() ,理由见解析;(4)4+
,理由见解析;(4)4+![]() +
+![]() .
.
【解析】
(1)利用勾股定理求出BC、AE,再利用直角三角形斜边上的中线等于斜边的一半即可求出结论;
(2)连接DP并延长交AB的延长线于F,利用AAS证出△FBP≌△DEP,从而求出AF和AD,利用勾股定理求出DF,再利用直角三角形斜边上的中线等于斜边的一半即可求出结论;
(3)连接DP并延长交AB的延长线于点H,利用AAS证出△PBH≌△PED,从而求出AH和AD,利用勾股定理求出DH,再利用直角三角形斜边上的中线等于斜边的一半即可求出结论;
(4)连接DP并延长交AB的延长线于点H,作DK⊥BA交BA的延长线于点K,过点A作AN⊥DH于点N,过点E作EM⊥BC交BC的延长线于点M,利用勾股定理、锐角三角函数和相似三角形的判定及性质求出PB和PA即可求出结论.
解:(1)∵∠ACB=90°,AC=3,AB=5,
∴BC=![]()
∵E是BC的中点,
∴CE=![]() BC=2
BC=2
∴AE=![]()
∵P是AE的中点,
∴CP=![]() AE=
AE=![]()
故答案为: ![]() ;
;
(2)连接DP并延长交AB的延长线于F
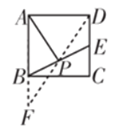
∵E是正方形ABCD一边上的中点,AB=4
∴AB=CD=AD=4,AB∥CD,∠BAD=90°
∴DE=![]() CD=2,∠F=∠PDE,∠FBP=∠DEP
CD=2,∠F=∠PDE,∠FBP=∠DEP
∵P是BE上的中点,
∴BP=EP
∴△FBP≌△DEP
∴FP=DP,BF=DE=2
∴AF=AB+BF=6
在Rt△ADF中,DF=![]()
∴AP=![]() DF=
DF=![]()
故答案为:![]() ;
;
(3)AP的长为![]() ,理由如下:
,理由如下:
如下图,连接DP并延长交AB的延长线于点H.
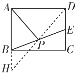
∵四边形ABCD是矩形,
∴AB∥CD,AB=CD=4,AD=BC=6,∠HAD=90°.
∴∠H=∠PDE.
∵P是BE上的中点,
∴BP=EP.
又∠BPH=∠EPD,
∴△PBH≌△PED(AAS).
∴BH=ED,HP=DP.
∵E是CD的中点,
∴BH=ED=CD=2.
∴AH=AB+BH=6.
在Rt△ADH中,DH=![]() ,
,
∴AP=![]() DH=
DH=![]() .
.
(4)如下图,连接DP并延长交AB的延长线于点H,作DK⊥BA交BA的延长线于点K,过点A作AN⊥DH于点N,过点E作EM⊥BC交BC的延长线于点M.
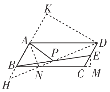
∵四边形ABCD是平行四边形,
∴∠BCD=∠BAD=120°,CD=AB=4,AD=BC=10.
在Rt△ADK中,∠KAD=180°-∠BAD=60°,∠K=90°,AD=10,
∴AK=AD·cos 60°=5,KD=AD·sin 60°=![]() .
.
在Rt△ECM中,∠M=90°,∠ECM=180°-∠BCD=60°,EC=![]() CD=2,
CD=2,
∴CM=EC·cos 60°=1,EM=EC·sin 60°=![]() .
.
在Rt△BEM中,BM=BC+CM=11,
∴BE=![]() =
=![]() .
.
∵P是BE的中点,
∴PB=![]() BE=
BE=![]() .
.
同(3)可得△PBH≌△PED,
∴HP=DP,HB=DE=![]() CD=2.
CD=2.
∴HK=HB+AB+AK=2+4+5=11,AH=AB+BH=6.
在Rt△HKD中,DH=![]() =14,
=14,
∴PH=PD=![]() DH=7.
DH=7.
∵∠AHN=∠DHK,∠ANH=∠K=90°,
∴△HAN∽△HDK.
∴![]() .
.
∴![]() .
.
∴AN=![]() ,HN=
,HN=![]() .
.
∴PN=PH-HN=7-![]() =
=![]() .
.
在Rt△APN中,PA=![]() =
= ,
,
∴△ABP的周长=AB+PA+PB=4+![]() +
+![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
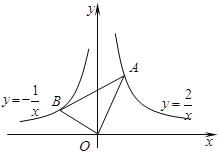
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数![]() 、
、![]() 的图象交于B、A两点,则∠OAB大小的变化趋势为( )
的图象交于B、A两点,则∠OAB大小的变化趋势为( )
A.逐渐变小B.逐渐变大C.时大时小D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=4:3时,求点D的坐标.
(3)如图2,点E的坐标为(0,-2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.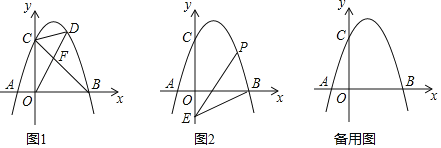
查看答案和解析>>
科目:初中数学 来源: 题型:
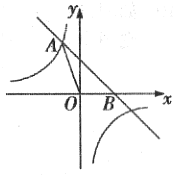
【题目】如图,直线y=﹣x+2与反比例函数y=![]() 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
(1)求该反比例函数的表达式;
(2)写出直线y=﹣x+2向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,作
,作![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作圆.
为半径作圆.
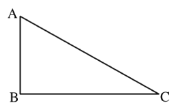
(1)依据题意补充完整图形;(尺规作图,保留作图痕迹,不写作法)
(2)求证:![]() 与直线
与直线![]() 相切;
相切;
(3)在(2)的条件下,若![]() 与直线
与直线![]() 相切的切点为
相切的切点为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ;其中
;其中![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
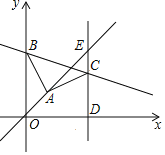
【题目】如图,平面直角坐标系中,A(4,4),B为y轴正半轴上一点,连接AB,在第一象限作AC=AB,∠BAC=90°,过点C作直线CD⊥x轴于D,直线CD与直线y=x交于点E,且ED=5EC,则直线BC解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
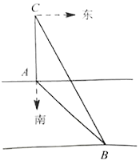
【题目】某数学活动小组实地测量某条河流两岸互相平行的一段东西走向的河的宽度.在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走40米到达点C处,测得点B在点C的南偏东27°方向,求这段河的宽度.(结果精确到1米.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市某中学开展以“三创一办”为中心,以“校园文明”为主题的手抄报比赛.同学们积极参与,参赛同学每人交了一份得意作品,所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如下两幅统计图.请你根据图中所给信息解答下列问题:
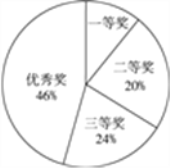

(1)一等奖所占的百分比是__________.
(2)在此次比赛中,一共收到多少份参赛作品?请将条形统计图补充完整.
(3)各奖项获奖学生分别有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com