练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

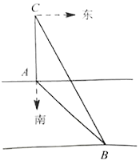
    【题目】某数学活动小组实地测量某条河流两岸互相平行的一段东西走向的河的宽度.在河的北岸边点A处，测得河的南岸边点B处在其南偏东45°方向，然后向北走40米到达点C处，测得点B在点C的南偏东27°方向，求这段河的宽度．（结果精确到1米．参考数据：，，，）

    【答案】42米

    【解析】

    如图，延长CA于点D，得CD⊥BD，设AD=x米，得BD=x米，CD=(40+x)米，在Rt△CBD中，根据=tan∠DCB列方程求出x的值即可得．

    如图，延长CA交于点D，

    则CD⊥BD，

    由题意知，∠DAB=45°，∠DCB=27°，

    设AD=x米，

    则BD=AD=x米，CD=(40+x)米，

    在在Rt△CBD中，=tan∠DCB，即=tan27°

    解得x≈42

    答：这段河的宽约为42米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

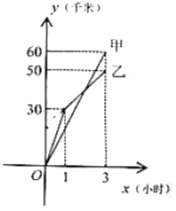
    【题目】如图反映了甲、乙两名自行车爱好者同时骑车从地到地进行训练时行驶路程（千米）和行驶时间（小时）之间关系的部分图像，根据图像提供的信息，解答下列问题：

    （1）求乙的行驶路程和行驶时间之间的函数解析式；

    （2）如果甲的速度一直保持不变，乙在骑行小时之后又以第小时的速度骑行，结果两人同时到达地，求、两地之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

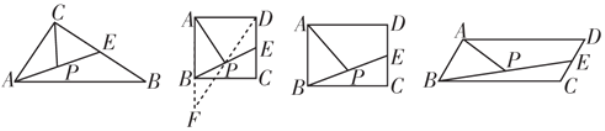
    【题目】（1）如图1，在△ABC中，E是BC的中点，P是AE的中点，则称CP是△ABC的“双中线”．若∠ACB＝90°，AC＝3，AB＝5，则CP＝________；

    （2）在图2中，E是正方形ABCD一边上的中点，P是BE上的中点，则称AP是正方形ABCD的“双中线”．若AB＝4，则AP的长为__________；（按图示辅助线求解）

    （3）在图3中，AP是矩形ABCD的“双中线”．若AB＝4，BC＝6，请仿照（2）中的方法求出AP的长，并说明理由；

    （4）在图4中，AP是□ABCD的“双中线”，若AB＝4，BC＝10，∠BAD＝120°，求△ABP的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，平行四边形内有两个全等的正六边形，若阴影部分的面积记为，平行四边形的面积记为,则的值为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

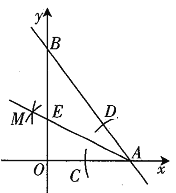
    【题目】如图，的直角边在x轴上，在y轴的正半轴上，且，，按以下步骤作图：①以点A为圆心，适当长度为半径作弧，分别交，于点C，D；②分别以C，D为圆心，大于的长为半径作弧，两弧在内交于点M；③作射线，交y轴于点E，则点E的坐标为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了测量一个铁球的直径，将该铁球放入工件槽内，测得的有关数据如图所示（单位：cm），则该铁球的直径为（ ）

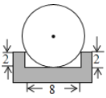
    A.12 cmB.10 cmC.8 cmD.6 cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】黄石市在创建国家级文明卫生城市中，绿化档次不断提升．某校计划购进A，B两种树木共100棵进行校园绿化升级，经市场调查：购买A种树木2棵，B种树木5棵，共需600元；购买A种树木3棵，B种树木1棵，共需380元．

    （1）求A种，B种树木每棵各多少元？

    （2）因布局需要，购买A种树木的数量不少于B种树木数量的3倍．学校与中标公司签订的合同中规定：在市场价格不变的情况下（不考虑其他因素），实际付款总金额按市场价九折优惠，请设计一种购买树木的方案，使实际所花费用最省，并求出最省的费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，AB=5，BC=4，E是BC边上一点，连接DE，将矩形ABCD沿DE折叠，顶点C恰好落在AB边上点F处，延长DE交AB的延长线于点G．

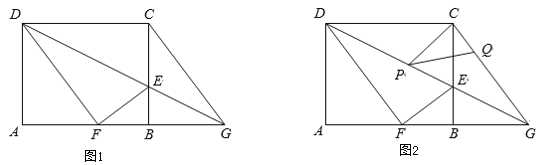
    （1）求线段BE的长；

    （2）连接CG，求证：四边形CDFG是菱形；

    （3）如图2，P，Q分别是线段DG，CG上的动点（与端点不重合），且∠CPQ=∠CDP，是否存在这样的点P，使△CPQ是等腰三角形？若存在，请直接写出DP的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

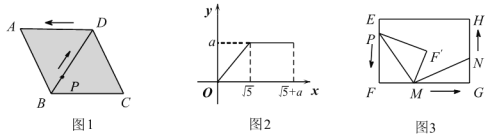
    【题目】如图1，点P从菱形ABCD的顶点B出发，沿B→D→A匀速运动到点A，BD的长是；图2是点P运动时，△PBC的面积y(cm2)随时间x(s)变化的函数图像．

    (1)点P的运动速度是 cm/s；

    (2)求a的值；

    (3)如图3，在矩形EFGH中，EF＝2a，FG－EF＝1，若点P、M、N分别从点E、F、G三点同时出发，沿矩形的边按逆时针方向匀速运动，当点M到达点G(即点M与点G重合)时，三个点随之停止运动；若点P不改变运动速度，且点P、M、N的运动速度的比为2:6:3，在运动过程中，△PFM关于直线PM的对称图形是△PF'M，设点P、M、N的运动时间为t(单位：s)．

    ①当t＝ s时，四边形PFMF'为正方形；

    ②是否存在t，使△PFM与△MGN相似，若存在，求t的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案