
【题目】(模型介绍)
古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营![]() .他总是先去
.他总是先去![]() 营,再到河边饮马,之后,再巡查
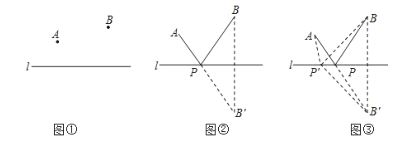
营,再到河边饮马,之后,再巡查![]() 营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点
营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连结
,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线
的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线![]() 上另取任一点
上另取任一点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,∵直线
,∵直线![]() 是点
是点![]() ,
,![]() 的对称轴,点
的对称轴,点![]() ,
,![]() 在
在![]() 上,
上,
(1)∴![]() __________,
__________,![]() _________,∴
_________,∴![]() ____________.在
____________.在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,即
,即![]() 最小.
最小.
(归纳总结)
在解决上述问题的过程中,我们利用轴对称变换,把点![]() 在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点
在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点![]() 为
为![]() 与
与![]() 的交点,即
的交点,即![]() ,
,![]() ,
,![]() 三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
(模型应用)
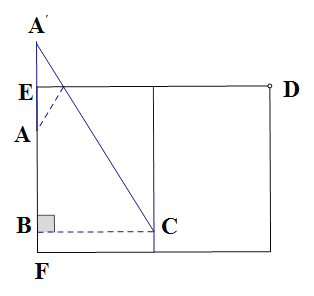
(2)如图④,正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上一动点.求
上一动点.求![]() 的最小值.
的最小值.
解析:解决这个问题,可借助上面的模型,由正方形对称性可知,点![]() 与
与![]() 关于直线
关于直线![]() 对称,连结
对称,连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的最小值就是线段
的最小值就是线段![]() 的长度,则
的长度,则![]() 的最小值是__________.
的最小值是__________.

(3)如图⑤,圆柱形玻璃杯,高为![]() ,底面周长为
,底面周长为![]() ,在杯内离杯底
,在杯内离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿![]() 与蜂蜜相对的点
与蜂蜜相对的点![]() 处,则蚂蚁到达蜂的最短路程为_________
处,则蚂蚁到达蜂的最短路程为_________![]() .
.

(4)如图⑥,在边长为2的菱形![]() 中,
中,![]() ,将
,将![]() 沿射线
沿射线![]() 的方向平移,得到
的方向平移,得到![]() ,分别连接
,分别连接![]() ,
,![]() ,
,![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.

【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)17;(4)
;(3)17;(4)![]()
【解析】
(1)根据对称性即可求解;
(2)根据正方形的对称性知B关于AC的对称点是D,连接ED,则ED是![]() 的最小值;
的最小值;
(3)先将玻璃杯展开,再根据勾股定理求解即可;
(4)分析知:当![]() 与
与![]() 垂直时,
垂直时,![]() 值最小,再根据特殊角计算长度即可;
值最小,再根据特殊角计算长度即可;
解:(1)根据对称性知:![]() ,
,
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)根据正方形的对称性知B关于AC的对称点是D,连接ED
∴ED是![]() 的最小值
的最小值
又∵正方形的边长为4,E是AB中点
∴![]()
∴![]() 的最小值是
的最小值是![]() ;
;
(3)由图可知:蚂蚁到达蜂的最短路程为![]() 的长度:
的长度:
∵![]()
∴![]()
∴![]()
(4)∵在边长为2的菱形ABCD中,![]() ,将
,将![]() 沿射线
沿射线![]() 的方向平移,得到
的方向平移,得到![]()
∴![]()
当![]() 与
与![]() 垂直时,
垂直时,![]() 值最小
值最小
∵![]()
∴四边形![]() 是矩形,
是矩形,![]()
∴![]()
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
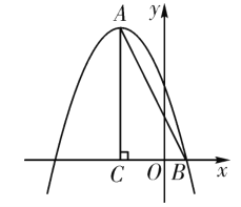
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一点,过点
上方抛物线上的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,使
,使![]() .
.
①求点![]() 的坐标和
的坐标和![]() 的面积;
的面积;
②在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?若存在,直接写出符合条件的所有点
为直角三角形?若存在,直接写出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
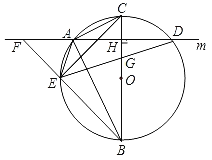
【题目】如图,在⊙O的内接△ABC中,∠CAB=90°,AB=2AC,过点A作BC的垂线m交⊙O于另一点D,垂足为H,点E为![]() 上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
(1)求证:△FED∽△AEB;
(2)若![]() =
=![]() ,AC=2,连接CE,求AE的长;
,AC=2,连接CE,求AE的长;
(3)在点E运动过程中,若BG=![]() CG,求tan∠CBF的值.
CG,求tan∠CBF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
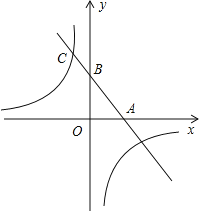
【题目】如图,一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=﹣![]() 的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
(1)求点C的坐标及k、b的值.
(2)求出一次函数图象与反比例函数图象的另一个交点的坐标,并直接写出当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:
表示,共分成四组:![]() .
.![]()
![]() .
.![]() C.
C.![]() D.
D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
八年级10名学生的竞赛成绩在![]() 组中的数据是:94,90,94
组中的数据是:94,90,94
八年级抽取的学生竞赛成绩扇形统计图:
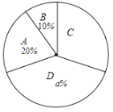
七、八年级抽取的学生竞赛成绩统计表:
年级 | 七年级 | 八年级 |
平均数 |
| 92 |
中位数 | 93 | 94 |
众数 | 99 | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中![]() 的值;
的值;
(2)根据以上数据,你认为该校七、八年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(![]() )的学生人数是多少?
)的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
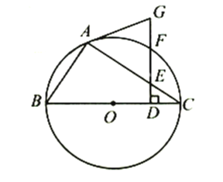
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“半日走遍江淮大地,安徽风景尽在徽园”,位于省会合肥的徽园景点某年三月共接待游客![]() 万人,四月比三月旅游人数增加了
万人,四月比三月旅游人数增加了![]() ,五月比四月游客人数增加了
,五月比四月游客人数增加了![]() ,已知三月至五月徽园的游客人数平均月增长率为
,已知三月至五月徽园的游客人数平均月增长率为![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() =
=![]() (
(![]() ≠0)图象如图所示,下列结论:①
≠0)图象如图所示,下列结论:①![]() >0;②
>0;②![]() =0;③当
=0;③当![]() ≠1时,
≠1时,![]() >
>![]() ;④
;④![]() >0;⑤若
>0;⑤若![]() =
=![]() ,且
,且![]() ≠
≠![]() ,则
,则![]() =2.其中正确的有( )
=2.其中正确的有( )
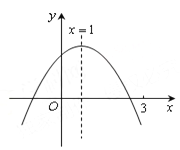
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各图形都是由同样大小的圆和正三角形按一定的规律组成.其中,第①个图形由8个圆和1个正三角形组成,第②个图形由16个圆和4个正三角形组成,第③个图形由24个圆和9个正三角形组成,……则第_____个图形中圆和正三角形的个数相等 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com