
【题目】如图,一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=﹣![]() 的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
(1)求点C的坐标及k、b的值.
(2)求出一次函数图象与反比例函数图象的另一个交点的坐标,并直接写出当![]() 时,x的取值范围.
时,x的取值范围.
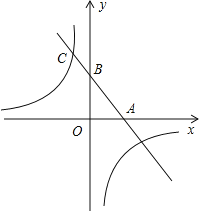
【答案】(1)C(﹣2,4);![]() ;(2)另一个交点坐标为(4,﹣2),x的取值范围为x<﹣2或0<x<4.
;(2)另一个交点坐标为(4,﹣2),x的取值范围为x<﹣2或0<x<4.
【解析】
(1)由A(2,0)利用平行线等分线段定理,可求出点C的横坐标,代入反比例函数关系式,可求其纵坐标;用两点法确定一次函数的关系式,即待定系数法确定函数的关系式,求出k、b的值;
(2)可将两个函数的关系式联立成方程组,解出方程组的解,若有两组解,说明两个函数的图象有两个交点,根据图象可以直观看出一次函数值大于反比例函数值时,自变量的取值范围.
(1)过点C作CD⊥x轴,垂足为D,
∵CD∥OB,
∴![]() ,
,
又∵B是AC的中点.
∴AB=BC,
∴OA=OD
∵A(2,0),
∴OA=OD=2,
当x=﹣2时,y=﹣![]() =4,
=4,
∴C(﹣2,4)
把A(2,0),C(﹣2,4)代入y=kx+b得:
![]() 解得:
解得:![]() ,
,
∴一次函数的关系式为:y=﹣x+2;
因此:C(﹣2,4),k=﹣1,b=2.
(2)由题意得:
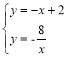 解得:
解得:![]() ;
;
∵一个交点C(﹣2.4)
∴另一个交点E(4,﹣2);
当![]() 时,即:y一次函数>y反比例函数,
时,即:y一次函数>y反比例函数,
由图象可以直观看出自变量x的取值范围:x<﹣2或0<x<4.
因此:另一个交点坐标为(4,﹣2),x的取值范围为x<﹣2或0<x<4.


科目:初中数学 来源: 题型:
【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
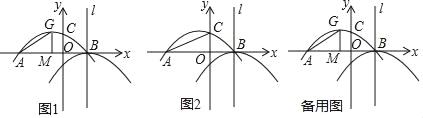
(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如何将一个长为17,宽为1的长方形经过剪一剪,拼一拼,形成一个正方形.(下列所有图中每个小方格的边长都为1,剪拼过程中材料均无剩余)
问题探究:我们从长为5,宽为1的长方形入手.
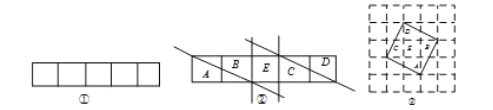
(1)如图①是一个长为5,宽为1的长方形.把这个长方形剪一剪、拼一拼后形成正方形,则正方形的面积应为_____________,设正方形的边长为![]() ,则
,则![]() _________;
_________;
(2)我们可以把有些带根号的无理数的被开方数表示成两个正整数平方和的形式,比如![]() .类比此,可以将(1)中的
.类比此,可以将(1)中的![]() 表示成
表示成![]() _____________;
_____________;
(3)![]() 的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为
的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为![]() ;类比此,(2)中的
;类比此,(2)中的![]() 可以理解为以长度________和__________为直角边的直角三角形斜边的长;
可以理解为以长度________和__________为直角边的直角三角形斜边的长;
(4)剪一剪:由(3)可画出如图②的分割线,把长方形分成![]() 五部分;
五部分;
(5)拼一拼:把图②中五部分拼接得到如图③的正方形;
问题解决:仿照上面的探究方法请把图④中长为17,宽为1的长方形剪一剪,在图⑤中画出拼成的正方形.(说明:图④的分割过程不作评分要求,只对图⑤中画出的最终结果评分)
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.

(1)、求证:BC 2=BDBA;
(2)、判断DE与⊙O位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020春节期间,一场突如其来的新冠肺炎疫情牵动着全国人民的心,因疫情发展迅速,全国口罩防护用品销售量暴涨、供应紧张,国有疫,我有责,在特殊时期,某集团紧急启动了应急响应机制,取消了工人休假,与疫情救灾相关的口罩、防护服生产线连续24小时运转,将援驰武汉的120万片口罩和8万防护服第一时间发往武汉,其中120万用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(模型介绍)
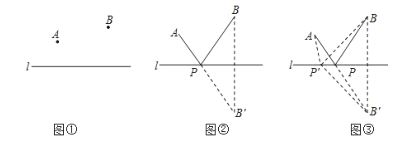
古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营![]() .他总是先去
.他总是先去![]() 营,再到河边饮马,之后,再巡查
营,再到河边饮马,之后,再巡查![]() 营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点
营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连结
,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线
的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线![]() 上另取任一点
上另取任一点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,∵直线
,∵直线![]() 是点
是点![]() ,
,![]() 的对称轴,点
的对称轴,点![]() ,
,![]() 在
在![]() 上,
上,
(1)∴![]() __________,
__________,![]() _________,∴
_________,∴![]() ____________.在
____________.在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,即
,即![]() 最小.
最小.
(归纳总结)
在解决上述问题的过程中,我们利用轴对称变换,把点![]() 在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点
在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点![]() 为
为![]() 与
与![]() 的交点,即
的交点,即![]() ,
,![]() ,
,![]() 三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
(模型应用)
(2)如图④,正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上一动点.求
上一动点.求![]() 的最小值.
的最小值.
解析:解决这个问题,可借助上面的模型,由正方形对称性可知,点![]() 与
与![]() 关于直线
关于直线![]() 对称,连结
对称,连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的最小值就是线段
的最小值就是线段![]() 的长度,则
的长度,则![]() 的最小值是__________.
的最小值是__________.

(3)如图⑤,圆柱形玻璃杯,高为![]() ,底面周长为
,底面周长为![]() ,在杯内离杯底
,在杯内离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿![]() 与蜂蜜相对的点
与蜂蜜相对的点![]() 处,则蚂蚁到达蜂的最短路程为_________
处,则蚂蚁到达蜂的最短路程为_________![]() .
.

(4)如图⑥,在边长为2的菱形![]() 中,
中,![]() ,将
,将![]() 沿射线
沿射线![]() 的方向平移,得到
的方向平移,得到![]() ,分别连接
,分别连接![]() ,
,![]() ,
,![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果连锁店销售某种热带水果,其进价为20元/千克.销售一段时间后发现:该水果的日销量![]() (千克)与售价
(千克)与售价![]() (元/千克)的函数关系如图所示:
(元/千克)的函数关系如图所示:
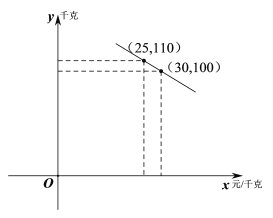
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?
(3)由于某种原因,该水果进价提高了![]() 元/千克(
元/千克(![]() ),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是
),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是![]() 元,请直接写出
元,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com