
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.

(1)、求证:BC 2=BDBA;
(2)、判断DE与⊙O位置关系,并说明理由.
【答案】(1)、证明过程见解析;(2)、相切;理由见解析.
【解析】
试题分析:(1)、根据直径可得∠ADC=∠BDC=90° 根据∠ACB=90° ∠B=∠B得出△BCD和△BAC相似,从而得出结论;(2)、连接OD,根据直角三角形斜边上的中线的性质得出∠EDC=∠ECD,根据OD=OC得出∠ODC=∠OCD,根据∠OCD+∠DCE=90°得出∠EDC+∠ODC=90°,从而说明∠EDO=90°,得出相切.
试题解析:(1)∵AC为![]() 的直径. ∴
的直径. ∴![]() ∴
∴![]()
又∵![]() ∴
∴![]() 又∵
又∵![]()
∴△BCD∽△BAC ∴![]() 即
即![]()
(2)、DE与![]() 相切 连结DO
相切 连结DO
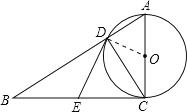
∵![]() ,E为BC的中点.
,E为BC的中点.
∴![]() ∴∠EDC=∠ECD
∴∠EDC=∠ECD
又∵在![]() 中,OD=OC ∴
中,OD=OC ∴![]() 而
而![]()
∴![]() 即
即![]() ∴
∴![]()
又∵点D在![]() 上 ∴DE与
上 ∴DE与![]() 相切
相切


科目:初中数学 来源: 题型:
【题目】解决问题.
学校要购买A,B两种型号的足球,按体育器材门市足球销售价格(单价)计算:若买2个A型足球和3个B型足球,则要花费370元,若买3个A型足球和1个B型足球,则要花费240元.
(1)求A,B两种型号足球的销售价格各是多少元/个?
(2)学校拟向该体育器材门市购买A,B两种型号的足球共20个,且费用不低于1300元,不超过1500元,则有哪几种购球方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
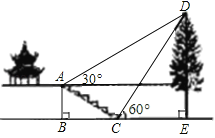
【题目】如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中∠BAC=90,E,F分别是BC,AC的中点,延长BA到点D,使AD=![]() AB,连接DE,DF。
AB,连接DE,DF。
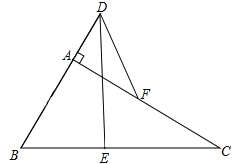
(1)试说明AF与DE互相平分;
(2)若BC=4,求DF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设抛物线C1:y=x2向右平移2个单位长度,再向下平移3个单位长度得到抛物线C2,则抛物线C2对应的函数解析式是( )
A. y=(x﹣2)2﹣3 B. y=(x+2)2﹣3 C. y=(x﹣2)2+3 D. y=(x+2)2+3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com