
【题目】“半日走遍江淮大地,安徽风景尽在徽园”,位于省会合肥的徽园景点某年三月共接待游客![]() 万人,四月比三月旅游人数增加了
万人,四月比三月旅游人数增加了![]() ,五月比四月游客人数增加了
,五月比四月游客人数增加了![]() ,已知三月至五月徽园的游客人数平均月增长率为
,已知三月至五月徽园的游客人数平均月增长率为![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
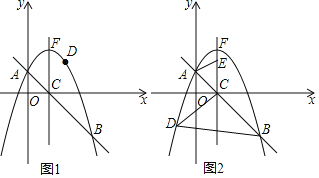
【题目】如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.
(1)求抛物线的函数表达式;
(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;
(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.

(1)、求证:BC 2=BDBA;
(2)、判断DE与⊙O位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
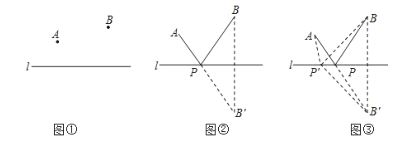
【题目】(模型介绍)
古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营![]() .他总是先去
.他总是先去![]() 营,再到河边饮马,之后,再巡查
营,再到河边饮马,之后,再巡查![]() 营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点
营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连结
,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线
的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线![]() 上另取任一点
上另取任一点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,∵直线
,∵直线![]() 是点
是点![]() ,
,![]() 的对称轴,点
的对称轴,点![]() ,
,![]() 在
在![]() 上,
上,
(1)∴![]() __________,
__________,![]() _________,∴
_________,∴![]() ____________.在
____________.在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,即
,即![]() 最小.
最小.
(归纳总结)
在解决上述问题的过程中,我们利用轴对称变换,把点![]() 在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点
在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点![]() 为
为![]() 与
与![]() 的交点,即
的交点,即![]() ,
,![]() ,
,![]() 三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
(模型应用)
(2)如图④,正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上一动点.求
上一动点.求![]() 的最小值.
的最小值.
解析:解决这个问题,可借助上面的模型,由正方形对称性可知,点![]() 与
与![]() 关于直线
关于直线![]() 对称,连结
对称,连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的最小值就是线段
的最小值就是线段![]() 的长度,则
的长度,则![]() 的最小值是__________.
的最小值是__________.

(3)如图⑤,圆柱形玻璃杯,高为![]() ,底面周长为
,底面周长为![]() ,在杯内离杯底
,在杯内离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿![]() 与蜂蜜相对的点
与蜂蜜相对的点![]() 处,则蚂蚁到达蜂的最短路程为_________
处,则蚂蚁到达蜂的最短路程为_________![]() .
.

(4)如图⑥,在边长为2的菱形![]() 中,
中,![]() ,将
,将![]() 沿射线
沿射线![]() 的方向平移,得到
的方向平移,得到![]() ,分别连接
,分别连接![]() ,
,![]() ,
,![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
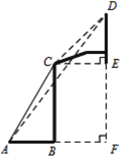
【题目】如图所示,一副篮架由配重、支架、篮板与篮筐组成,在立柱的C点观察篮板上沿D点的仰角为45°,在支架底端的A点观察篮板上沿D点的仰角为54°,点C与篮板下沿点E在同一水平线,若AB=1.91米,篮板高度DE为1.05米,求篮板下沿E点与地面的距离.(结果精确到0.1m,参考数据:sin54°≈0.80, cos54°≈0.60,tan54°≈1.33)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果连锁店销售某种热带水果,其进价为20元/千克.销售一段时间后发现:该水果的日销量![]() (千克)与售价
(千克)与售价![]() (元/千克)的函数关系如图所示:
(元/千克)的函数关系如图所示:
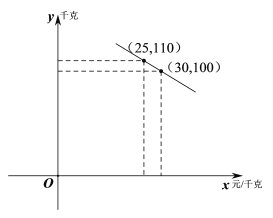
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?
(3)由于某种原因,该水果进价提高了![]() 元/千克(
元/千克(![]() ),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是
),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是![]() 元,请直接写出
元,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙![]() 中,AB是直径,BC是弦,BC=BD,连接CD交⊙
中,AB是直径,BC是弦,BC=BD,连接CD交⊙![]() 于点E,∠BCD=∠DBE.
于点E,∠BCD=∠DBE.
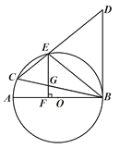
(1)求证:BD是⊙![]() 的切线.
的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=![]() ,EG=3,求BG的长.
,EG=3,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com