
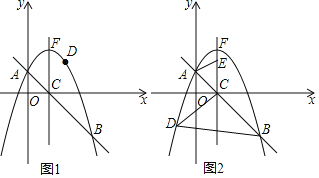
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌНЋХзЮяЯпyЃНЉx2+bx+cгыжБЯпyЃНЉx+1ЯрНЛгкЕуA(0ЃЌ1)КЭЕуB(3ЃЌЉ2)ЃЌНЛxжсгкЕуCЃЌЖЅЕуЮЊЕуFЃЌЕуDЪЧИУХзЮяЯпЩЯвЛЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌШєЕуDдкжБЯпABЩЯЗНЕФХзЮяЯпЩЯЃЌЧѓЁїDABЕФУцЛ§зюДѓЪБЕуDЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуDдкЖдГЦжсзѓВрЕФХзЮяЯпЩЯЃЌЧвЕуEЃЈ1ЃЌtЃЉЪЧЩфЯпCFЩЯвЛЕуЃЌЕБвдCЁЂBЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїCAEЯрЫЦЪБЃЌЧѓЫљгаТњзуЬѕМўЕФtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+2x+1ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉtЃН1ЛђtЃН2Лђ
ЃЛЃЈ3ЃЉtЃН1ЛђtЃН2Лђ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAЃЈ0ЃЌ1ЃЉКЭЕуBЃЈ3ЃЌ-2ЃЉДњШыХзЮяЮяЯпy=-x2+bx+cжаЃЌСаГіЗНГЬзщМДПЩНтД№ЃЛ
ЃЈ2ЃЉЙ§ЕуDзї DMЁЮyжсНЛABгкЕуMЃЌDЃЈaЃЌ-a2+2a+1ЃЉЃЌдђMЃЈaЃЌ-a+1ЃЉЃЌБэДяГіDMЃЌНјЖјБэДяГіЁїABDЕФУцЛ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪЕУГізюДѓжЕМАDЕузјБъЃЛ
ЃЈ3ЃЉгЩЬтвтПЩжЊЃЌЁЯACE=ЁЯACO=45ЁуЃЌдђЁїBCDжаБигавЛИіФкНЧЮЊ45ЁуЃЌгаСНжжЧщПіЃКЂйШєЁЯCBD=45ЁуЃЌЕУГіЁїBCDЪЧЕШбќжБНЧШ§НЧаЮЃЌвђДЫЁїACEвВЪЧЕШбќжБНЧШ§НЧаЮЃЌдйЁїACEНјааЗжРрЬжiТлЃЛЂкШєЁЯCDB=45ЃЌИљРЈдВЕФаджЪШЗЖЈD1ЕФЮЛжУЃЌЧѓГіD1ЕФзјБъЃЌдйЖдЁїACEгыЁїCD1BЯрЫЦЗжРрЬжТлЃЎ
НтЃКЃЈ1ЃЉНЋЕуAЃЈ0ЃЌ1ЃЉКЭЕуBЃЈ3ЃЌЉ2ЃЉДњШыХзЮяЮяЯпyЃНЉx2+bx+cжа
ЕУ![]() ЃЌ
ЃЌ
НтЕУ![]()
ЁрyЃНЉx2+2x+1ЃЛ
ЃЈ2ЃЉШчЭМ1ЫљЪОЃКЙ§ЕуDзї DMЁЮyжсНЛABгкЕуMЃЌ
ЩшDЃЈaЃЌЉa2+2a+1ЃЉЃЌдђMЃЈaЃЌЉa+1ЃЉ
ЃЎЁрDMЃНЉa2+2a+1ЉЃЈЉa+1ЃЉЃНЉa2+3a
Ёр![]()
Ёп![]()
![]() ЃЌ
ЃЌ![]() газюДѓжЕЃЌ
газюДѓжЕЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ДЫЪБ![]()

ЭМ1
ЃЈ3ЃЉЁпOAЃНOCЃЌШчЭМ2ЃЌCFЁЮyжсЃЌ
ЁрЁЯACEЃНЁЯACOЃН45ЁуЃЌ
ЁрЁїBCDжаБигавЛИіФкНЧЮЊ45ЁуЃЌгЩЬтвтПЩжЊЃЌЁЯBCDВЛПЩФмЮЊ45ЁуЃЌ
ЂйШєЁЯCBDЃН45ЁуЃЌдђBDЁЮxжсЃЌ
ЁрЕуDгыЕуBгкХзЮяЯпЕФГЦжсжБЯпxЃН1ГЦЃЌЩшBDгыжБЯпЃН1НЛгкЕуHЃЌдђHЃЈ1ЃЌЉ2ЃЉ
BЃЈ3ЃЌЉ2ЃЉЃЌDЃЈЉ1ЃЌЉ2ЃЉ
ДЫЪБЁїBCDЪЧЕШбќжБНЧШ§НЧаЮЃЌвђДЫЁїACEвВЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЃЈiЃЉЕБЁЯAECЃН90ЁуЪБЃЌЕУЕНAEЃНCEЃН1ЃЌ
ЁрEЃЈ1.1ЃЉЃЌЕУЕНtЃН
ЃЈiiЃЉЕБЁЯCAEЃН90ЪБЃЌЕУЕНЃКACЃНAEЃН![]() ЃЌ
ЃЌ
ЁрCEЃН2ЃЌЁрEЃЈ1.2ЃЉЃЌЕУЕНtЃН2
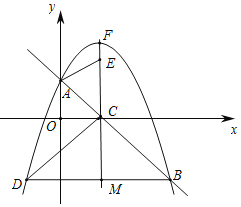
ЭМ2
ЂкШєЁЯCDBЃН45ЁуЃЌШчЭМ3ЃЌЂйжаЕФЧщПіЪЧЦфжавЛжжЃЌД№АИЭЌЩЯ
вдЕуHЮЊдВаФЃЌHBЮЊАыОЖзїдВЃЌдђЕуBЁЂCЁЂDЖМдкдВHЩЯЃЌ
ЩшдВHгыЖдГЦзѓВрЕФЮяЯпНЛгкСэвЛЕуD1ЃЌ
дђЁЯCD1BЃНЁЯCDBЃН45ЁуЃЈЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШЃЉЃЌМДD1вВЗћКЯЬтвт
Щш![]()
гЩHD1ЃНDHЃН2
НтЕУn1ЃНЉ1ЃЈКЌШЅЃЉЃЌn2ЃН3ЃЈЩсШЅЃЉЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]()
Ёр![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
![]()
ЃЈiЃЉШєЁїACEЁзЁїCD1BЃЌ
дђ![]() ЃЌ
ЃЌ
МД ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЃЈiiЃЉЁїACEЁзЁїBD1Cдђ![]() ЃЌ
ЃЌ
МД ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
злЩЯЫљЪіЃКЫљгаТњзуЬѕМўЕФtЕФжЕЮЊtЃН1ЛђtЃН2Лђ![]() Лђ
Лђ![]()

ЭМ3


 ЦпВЪЬтПЈПкЫугІгУвЛЕуЭЈЯЕСаД№АИ
ЦпВЪЬтПЈПкЫугІгУвЛЕуЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдчГПЃЌаЁИебизХЭЈЭљбЇаЃЮЈвЛЕФвЛЬѕТЗЃЈжБТЗЃЉЩЯбЇЃЌЭОжаЗЂЯжЭќДјЗЙКаЃЌЭЃЯТРДЭљМвРяДђЕчЛАЃЌТшТшНгЕНЕчЛАКѓДјЩЯЗЙКаТэЩЯИЯЭљбЇаЃЃЌЭЌЪБаЁИеЗЕЛиЃЌСНШЫЯргіКѓЃЌаЁИеСЂМДИЯЭљбЇаЃЃЌТшТшЛиМвЃЌ15ЗжжгКѓТшТшЕНМвЃЌдйОЙ§3ЗжжгаЁИеЕНДябЇаЃЃЌаЁИеЪМжевд100Уз/ЗжЕФЫйЖШВНааЃЌаЁИеКЭТшТшЕФОрРыyЃЈЕЅЮЛЃКУзЃЉгыаЁИеДђЭъЕчЛАКѓЕФВНааЪБМфtЃЈЕЅЮЛЃКЗжЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЃЌЯТСаЫФжжЫЕЗЈжаДэЮѓЕФЪЧЃЈ ЃЉ

A. ДђЕчЛАЪБЃЌаЁИеКЭТшТшЕФОрРыЮЊ1250Уз
B. ДђЭъЕчЛАКѓЃЌОЙ§23ЗжжгаЁИеЕНДябЇаЃ
C. аЁИеКЭТшТшЯргіКѓЃЌТшТшЛиМвЕФЫйЖШЮЊ150Уз/Зж
D. аЁИеМвгыбЇаЃЕФОрРыЮЊ2550Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФЖЅЕуPдкxжсЩЯЃЌгыyжсЯрНЛгкЕуAЃЎ
ЕФЖЅЕуPдкxжсЩЯЃЌгыyжсЯрНЛгкЕуAЃЎ
![]() Ђё
Ђё![]() ЧѓЕуAЕФзнзјБъ
ЧѓЕуAЕФзнзјБъ![]() гУКЌbЕФЪНзгБэЪО
гУКЌbЕФЪНзгБэЪО![]() ЃЛ
ЃЛ
![]() Ђђ
Ђђ![]() ЕБ
ЕБ![]() ЪБЃЌyгазюДѓжЕ9ЃЌЧѓbЕФжЕЃЛ
ЪБЃЌyгазюДѓжЕ9ЃЌЧѓbЕФжЕЃЛ
![]() Ђѓ
Ђѓ![]() ЕуBдкХзЮяЯпЩЯЃЌЧв
ЕуBдкХзЮяЯпЩЯЃЌЧв![]() ЃЌСЌНгABЃЌНЛЖдГЦжсгкЕуCЃЎ
ЃЌСЌНгABЃЌНЛЖдГЦжсгкЕуCЃЎ
![]() ЧѓжЄЃКPCЮЊЖЈГЄЃЛ
ЧѓжЄЃКPCЮЊЖЈГЄЃЛ
![]() жБНгаДГі
жБНгаДГі![]() УцЛ§ЕФзюаЁжЕЃЎ
УцЛ§ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєећЪ§aМШЪЙЕУЙигкxЕФЗжЪНЗНГЬ![]() гаЗЧИКЪ§НтЃЌгжЪЙЕУЙигкxЕФВЛЕШЪНx2-x+a+5Ён0КуГЩСЂЃЌдђЗћКЯЬѕМўЕФЫљгаaЕФИіЪ§ЮЊЃЈ ЃЉ
гаЗЧИКЪ§НтЃЌгжЪЙЕУЙигкxЕФВЛЕШЪНx2-x+a+5Ён0КуГЩСЂЃЌдђЗћКЯЬѕМўЕФЫљгаaЕФИіЪ§ЮЊЃЈ ЃЉ
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
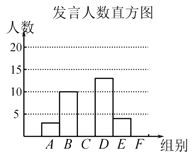
ЁОЬтФПЁП2020ФъДКНкЧАЯІЁАаТаЭЙкзДВЁЖОЁББЌЗЂЃЌЙњМвНЬг§ВПвЊЧѓИїЕибгЦкПЊбЇЃЌВЂвЊЧѓЃКРћгУЭјТчЦНЬЈЃЌЁАЭЃПЮВЛЭЃбЇЁБЃЎЮЊЯьгІКХейЃЌФГаЃЪІЩњИљОнЩЯМЖвЊЧѓЛ§МЋПЊеЙЭјТчЪкПЮНЬбЇЃЌАЫФъМЖЮЊСЫНтбЇЩњЭјПЮЗЂбдЧщПіЃЌЫцЛњГщШЁИУФъМЖВПЗжбЇЩњЃЌЖдЫћУЧФГЬьдкЭјПЮЩЯЗЂбдЕФДЮЪ§НјааСЫЭГМЦЃЌЦфНсЙћШчЯТБэЃЌВЂЛцжЦСЫШчЭМЫљЪОЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЌвбжЊBЁЂEСНзщЗЂбдШЫЪ§ЕФБШЮЊ5ЃК2ЃЌЧыНсКЯЭМжаЯрЙиЪ§ОнЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓГібљБОШнСПЃЌВЂВЙШЋжБЗНЭМЃЌдкЩШаЮЭГМЦЭМжаЃЌЁАBЁБЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЪЧ ЃЛ
ЃЈ2ЃЉИУФъМЖЙВгабЇЩњ500ШЫЃЌЙРМЦШЋФъМЖдкетЬьРяЗЂбдДЮЪ§ВЛЩйгк12ЕФШЫЪ§ЮЊ ЃЛ
ЃЈ3ЃЉИУаЃАЫФъМЖзщжЏвЛДЮЭјТчЪкПЮОбщзЈЯюЪгЦЕЛсвщЃЌAзщЕФжаЧЁга1ЮЛХЎЩњЃЌEзщЕФжагаЮЛ2ФаЩњЃЎЯжДгAзщгыEзщжаЗжБ№ГщвЛЮЛаДБЈИцЃЌРћгУЁАЪїзДЭМЁБЛђСаБэЗЈЧѓГіе§КУбЁжавЛФавЛХЎЕФИХТЪЃЎ
n | |
A |
|
B |
|
C |
|
D |
|
E |
|
F |
|

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбСтаЮABCDбиAHелЕўЃЌBТфдкBCЩЯЕФЕуEДІЃЌШєЁЯBAEЃН40ЁуЃЌдђЁЯEDCЕФДѓаЁЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуOЁЂAЁЂCЕФзјБъЗжБ№ЮЊOЃЈ0ЃЌ0ЃЉЃЌAЃЈЉxЃЌ0ЃЉЃЌCЃЈ0ЃЌyЃЉЃЌЧвxЁЂyТњзу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉОиаЮЕФЖЅЕуBЕФзјБъЪЧЁЁ ЃЎ
ЃЈ2ЃЉШєDЪЧABжаЕуЃЌбиDOелЕўОиаЮOABCЃЌЪЙAЕуТфдкЕуEДІЃЌелКлЮЊDOЃЌСЌBEВЂбгГЄBEНЛyжсгкQЕуЃЎ
ЂйЧѓжЄЃКЫФБпаЮDBOQЪЧЦНааЫФБпаЮЃЎ
ЂкЧѓЁїOEQУцЛ§ЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєRдкЯпЖЮABЩЯЃЌARЃН4ЃЌPЪЧABзѓВрвЛЖЏЕуЃЌЧвЁЯRPAЃН135ЁуЃЌЧѓQPЕФзюДѓжЕЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBACЕФЦНЗжЯпADгыБпBCЕФДЙжБЦНЗжЯпEDЯрНЛгкЕуDЃЌЙ§ЕуDзїDFЁЭACНЛACбгГЄЯпгкЕуFЃЌШєAB=8ЃЌAC=4ЃЌдђCFЕФГЄЮЊ_________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
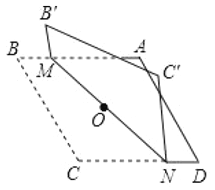
ЁОЬтФПЁПЖдНЧЯпГЄЗжБ№ЮЊ![]() КЭ
КЭ![]() ЕФСтаЮ
ЕФСтаЮ![]() ШчЭМЫљЪОЃЌЕу
ШчЭМЫљЪОЃЌЕу![]() ЮЊЖдНЧЯпЕФНЛЕуЃЎЙ§Еу
ЮЊЖдНЧЯпЕФНЛЕуЃЎЙ§Еу![]() елЕўСтаЮЃЌЪЙ
елЕўСтаЮЃЌЪЙ![]() СНЕужиКЯЃЌ
СНЕужиКЯЃЌ![]() ЪЧелКлЃЌШє
ЪЧелКлЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com