
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:
表示,共分成四组:![]() .
.![]()
![]() .
.![]() C.
C.![]() D.
D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
八年级10名学生的竞赛成绩在![]() 组中的数据是:94,90,94
组中的数据是:94,90,94
八年级抽取的学生竞赛成绩扇形统计图:
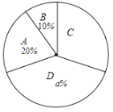
七、八年级抽取的学生竞赛成绩统计表:
年级 | 七年级 | 八年级 |
平均数 |
| 92 |
中位数 | 93 | 94 |
众数 | 99 | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中![]() 的值;
的值;
(2)根据以上数据,你认为该校七、八年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(![]() )的学生人数是多少?
)的学生人数是多少?
【答案】(1)![]() ,
,![]() ;(2)八年级,中位数大,高分多;(3)468
;(2)八年级,中位数大,高分多;(3)468
【解析】
(1)根据A,B两组对应的百分数可求出对应人数,再结合已知可得出D组的人数即可求出a值,根据七年级10名学生的竞赛成绩即可算出平均数;
(2)根据中位数和众数的数据进行判断即可;
(3)求出成绩优秀的人所占的百分比,再乘以总人数即可.
(1)A组:20%×10=2(人),B组:10%×10=1(人),
D组:10-2-1-3=4(人),
a%=![]() ×100%=40%,
×100%=40%,
故a=40,
b=![]() =92,
=92,
故答案为:40,92;
(2)八年级学生掌握防溺水安全知识较好,理由如下:
①七、八年级学生的竞赛成绩平均分相同,但八年级学生成绩的中位数94高于七年级学生的中位数93;
②七、八年级学生的竞赛成绩平均分相同,但八年级学生成绩的众数100高于七年级学生的众数99;
(3)∵七年级10名学生中,成绩在C,D两组中的有6人,八年级10名学生中,成绩在C,D两组中的有7人,
∴成绩优秀的人所占的百分比为:![]() ×100%=65%,
×100%=65%,
故720×65%=468(人).


科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN![]() 90°.
90°.
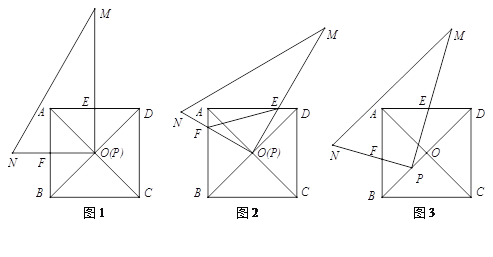
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗,若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM![]() 15°时,连接EF,若正方形的边长为2,请求出线段EF的长;
15°时,连接EF,若正方形的边长为2,请求出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD![]() 3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD
3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD![]() m·BP时,请直接写出PE与PF的数量关系.
m·BP时,请直接写出PE与PF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.
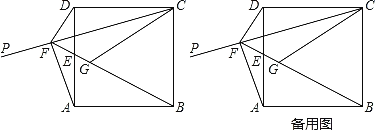
(1)试判断DF与BF的位置关系,并说明理由;
(2)若CF=4![]() ,DF=2,求AE的长;
,DF=2,求AE的长;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.

(1)、求证:BC 2=BDBA;
(2)、判断DE与⊙O位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
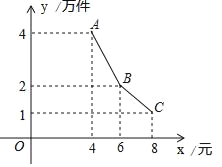
【题目】为了支持大学生创业,某市政府出台了一项优惠政策:提供10万元的无息创业贷款.小王利用这笔贷款,注册了一家淘宝网店,招收5名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款.已知该产品的成本为每件4元,员工每人每月的工资为4千元,该网店还需每月支付其它费用1万元.该产品每月销售量y(万件)与销售单价x(元)万件之间的函数关系如图所示.
(1)求该网店每月利润w(万元)与销售单价x(元)之间的函数表达式;
(2)小王自网店开业起,最快在第几个月可还清10万元的无息贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(模型介绍)
古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营![]() .他总是先去
.他总是先去![]() 营,再到河边饮马,之后,再巡查
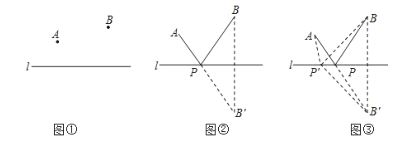
营,再到河边饮马,之后,再巡查![]() 营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点
营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连结
,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线
的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线![]() 上另取任一点
上另取任一点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,∵直线
,∵直线![]() 是点
是点![]() ,
,![]() 的对称轴,点
的对称轴,点![]() ,
,![]() 在
在![]() 上,
上,
(1)∴![]() __________,
__________,![]() _________,∴
_________,∴![]() ____________.在
____________.在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,即
,即![]() 最小.
最小.
(归纳总结)
在解决上述问题的过程中,我们利用轴对称变换,把点![]() 在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点
在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点![]() 为
为![]() 与
与![]() 的交点,即
的交点,即![]() ,
,![]() ,
,![]() 三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
(模型应用)
(2)如图④,正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上一动点.求
上一动点.求![]() 的最小值.
的最小值.
解析:解决这个问题,可借助上面的模型,由正方形对称性可知,点![]() 与
与![]() 关于直线
关于直线![]() 对称,连结
对称,连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的最小值就是线段
的最小值就是线段![]() 的长度,则
的长度,则![]() 的最小值是__________.
的最小值是__________.

(3)如图⑤,圆柱形玻璃杯,高为![]() ,底面周长为
,底面周长为![]() ,在杯内离杯底
,在杯内离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿![]() 与蜂蜜相对的点
与蜂蜜相对的点![]() 处,则蚂蚁到达蜂的最短路程为_________
处,则蚂蚁到达蜂的最短路程为_________![]() .
.

(4)如图⑥,在边长为2的菱形![]() 中,
中,![]() ,将
,将![]() 沿射线
沿射线![]() 的方向平移,得到
的方向平移,得到![]() ,分别连接
,分别连接![]() ,
,![]() ,
,![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
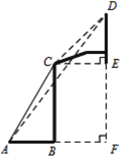
【题目】如图所示,一副篮架由配重、支架、篮板与篮筐组成,在立柱的C点观察篮板上沿D点的仰角为45°,在支架底端的A点观察篮板上沿D点的仰角为54°,点C与篮板下沿点E在同一水平线,若AB=1.91米,篮板高度DE为1.05米,求篮板下沿E点与地面的距离.(结果精确到0.1m,参考数据:sin54°≈0.80, cos54°≈0.60,tan54°≈1.33)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙![]() 中,AB是直径,BC是弦,BC=BD,连接CD交⊙
中,AB是直径,BC是弦,BC=BD,连接CD交⊙![]() 于点E,∠BCD=∠DBE.
于点E,∠BCD=∠DBE.
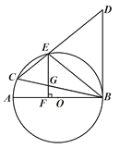
(1)求证:BD是⊙![]() 的切线.
的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=![]() ,EG=3,求BG的长.
,EG=3,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
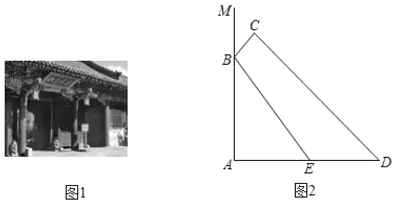
【题目】如图1,我国古建筑的大门上常常悬挂着巨大的匾额,图2中的线段![]() 就是悬挂在墙壁
就是悬挂在墙壁![]() 上的某块匾额的截面示意图.已知
上的某块匾额的截面示意图.已知![]() 米,
米,![]() .从水平地面点
.从水平地面点![]() 处看点
处看点![]() ,仰角
,仰角![]() ,从点
,从点![]() 处看点
处看点![]() ,仰角
,仰角![]() .且
.且![]() 米,求匾额悬挂的高度
米,求匾额悬挂的高度![]() 的长.(参考数据:
的长.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com