
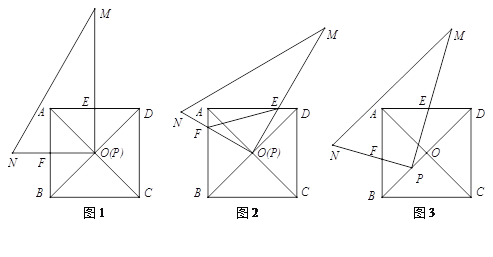
����Ŀ����������ABCD�У��Խ���AC��BD���ڵ�O����Rt��PMN�У���MPN![]() 90����
90����
��1����ͼ1������P���O�غ���PM��AD��PN��AB���ֱ�AD��AB�ڵ�E��F����ֱ��д��PE��PF��������ϵ��
��2����ͼ1�е�Rt��PMN�Ƶ�O˳ʱ����ת�Ƕ�����0��<��<45������
����ͼ2������ת�����У�1���еĽ�����Ȼ����������������֤����������������˵�����ɣ�
����ͼ2������ת�����У�����DOM![]() 15��ʱ������EF���������εı߳�Ϊ2��������߶�EF�ij���
15��ʱ������EF���������εı߳�Ϊ2��������߶�EF�ij���
����ͼ3����ת����Rt��PMN�Ķ���P���߶�OB���ƶ��������O��B�غϣ�����BD![]() 3BPʱ�������ʱPE��PF��������ϵ��������֤������BD
3BPʱ�������ʱPE��PF��������ϵ��������֤������BD![]() m��BPʱ����ֱ��д��PE��PF��������ϵ��
m��BPʱ����ֱ��д��PE��PF��������ϵ��
���𰸡���1��PE=PF����2�������������ɲμ���������![]() ����PE=2PF�����ɼ�������PE=��m-1����PF��
����PE=2PF�����ɼ�������PE=��m-1����PF��
��������
��1�����������ε����ʺͽ�ƽ���ߵ����ʽ�ɣ�
��2���ٸ��������ε����ʺ���ת������֤����FOA�ա�EOD���õ��𰸣�
����OG��AB��G���������ҵĸ������OF�ij������ݹ��ɶ�����ֵ���ɣ�
�۹���P��HP��BD��AB�ڵ�H���������������ε��ж����������PE��PF��������ϵ�����ݽ�����ܽ���ɵõ���BD=mBPʱ��PE��PF��������ϵ��
�⣺��1��PE=PF�����ɣ�
���ı���ABCDΪ�����Σ�
���BAC=��DAC����PM��AD��PN��AB��
��PE=PF��
��2���ٳ��������ɣ�
��AC��BD��������ABCD�ĶԽ��ߣ�
��OA=OD����FAO=��EDO=45������AOD=90����
���DOE+��AOE=90����
�ߡ�MPN=90����
���FOA+��AOE=90����
���FOA=��DOE��
����FOA����EOD�� ��
��
���FOA�ա�EOD��
��OE=OF����PE=PF��

����OG��AB��G��
�ߡ�DOM=15����
���AOF=15�������FOG=30����
��cos��FOG=![]() ��
��
��OF=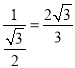 ��
��
��OE=OF��
��EF=![]() ��
��
��PE=2PF��
��ͼ3������P��HP��BD��AB�ڵ�H��

����HPBΪ����ֱ�������Σ���HPD=90����
��HP=BP��
��BD=3BP��
��PD=2BP��
��PD=2HP��
�֡ߡ�HPF+��HPE=90������DPE+��HPE=90����
���HPF=��DPE��
�֡ߡ�BHP=��EDP=45����
���PHF�ס�PDE��
��![]() ��
��
��PE=2PF��
�ɴ˹��ɿ�֪����BD=mBPʱ��PE=��m-1��PF��


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
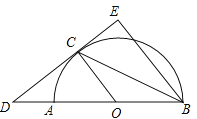
����Ŀ����ͼ����֪AB����O��ֱ����CD����O������C��BE��CO��
��1����֤��BC����ABE��ƽ���ߣ�
��2����DC=8����O�İ뾶OA=6����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѳ�Ϊ�ҹ���ú�硢ˮ��֮��ĵ������Դ����������Ҫ�����˺�ҶƬ��ɣ���ͼ1����ͼ2�Ǵ�ͼ1������ƽ��ͼ��������վ��A��������˶���C��������55�㣬��HA����ˮƽǰ��43����ɽ��G������ɽ��B����������һҶƬ�������λ�ã���ʱ���ҶƬ�Ķ���D��D��C��H��ͬһֱ���ϣ���������45�㣮��֪ҶƬ�ij���Ϊ35�ף�������ҶƬ���Ӵ��ij��Ⱥ��Բ��ƣ���ɽ��BGΪ10�ף�BG��HG��CH��AH��������CH�ĸߣ����ο����ݣ�tan55���1.4��tan35���0.7��sin55���0.8��sin35���0.6��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����2x+2����������ֱ���A��B���㣬���߶�OA�ֳ�n�ȷݣ��ֵ�ֱ�ΪP1��P2��P3������Pn��1����ÿ���ֵ���x��Ĵ��߷ֱ�ֱ��AB�ڵ�T1��T2��T3������Tn��1����S1��S2��S3������Sn��1�ֱ��ʾRt��T1OP1��Rt��T2P1P2������Rt��Tn��1Pn��2Pn��1���������n��2015ʱ��S1+S2+S3+��+Sn��1��_____��
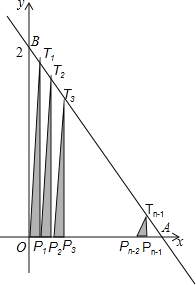
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
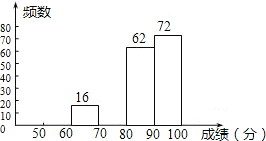
����Ŀ������п��������3000��ѧ���μӡ������л�֪ʶ�������Ļ��Ϊ���˽Ȿ��֪ʶ�����ijɼ��ֲ���������г�ȡ��200��ѧ���ĵ÷ֽ���ͳ�ƣ�������ݲ������ı��ش��������⣺
��1����ȫƵ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
��2�������÷�ת��Ϊ�ȼ����涨![]() ��Ϊ��
����![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ����
��Ϊ��![]() �������ȫ��μӾ�����ѧ���У��ж���ѧ�������ɼ�����Ϊ��
�������ȫ��μӾ�����ѧ���У��ж���ѧ�������ɼ�����Ϊ��![]() �������������һ������ѧ���ijɼ��ȼ���������ѧ���ijɼ�����һ���ȼ��Ŀ����Դ���˵�����ɣ�
�������������һ������ѧ���ijɼ��ȼ���������ѧ���ijɼ�����һ���ȼ��Ŀ����Դ���˵�����ɣ�
�ɼ� | Ƶ�� | Ƶ�� |
| 10 | |
| 16 | 0.08 |
| 0.2 | |
| 62 | |
72 | 0.36 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
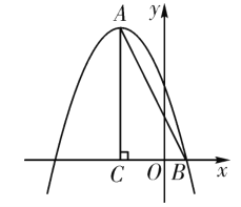
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ����
����![]() ������Ϊ
������Ϊ![]() ��������
��������![]() ����
����![]() ���㣮
���㣮
��1���������ߵĽ���ʽ��
��2����![]() ��ֱ��
��ֱ��![]() �Ϸ��������ϵ�һ�㣬����
�Ϸ��������ϵ�һ�㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() �����߶�
�����߶�![]() �ڵ�
�ڵ�![]() ��ʹ
��ʹ![]() ��
��
�����![]() �������
�������![]() �������
�������
����ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ
��ʹ![]() Ϊֱ�������Σ������ڣ�ֱ��д���������������е�
Ϊֱ�������Σ������ڣ�ֱ��д���������������е�![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��12������������ʡ�人�в���ҽԺ½�����ֲ���ԭ����ײ���������֤ʵ�÷���Ϊһ������״������Ⱦ�ķ��ף��䴫Ⱦ�Խ�ǿ��Ϊ����Ч�ر��⽻���Ⱦ����Ҫ��ȡ���·�����ʩ���ٴ����֣�����ϴ�֣����ٳ��ţ����ظ��룻����ڱǣ������ԣ�ij��˾Ϊ�˽�Ա���Է�����ʩ���˽�̶ȣ��������˽⡢�˽���١������˽�ͺ��˽⣩��ͨ�������ʾ�����ķ�ʽ����������������飨ÿ��Ա��������ֻ��ѡ��һ����������������Ƴ���������ͳ��ͼ��
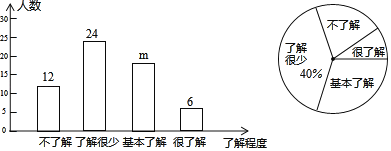
��������������Ϣ�������������
��1�����ι��������� ����Ա��������ͳ��ͼ��m���� ����
��2������ͳ��ͼ�С����˽⡱��������Ӧ��Բ�ĽǶ�����_____________��
��3�����ù�˾����Ա��1200����������Ʋ��˽������ʩ��������
��4���ڵ����У�������4��Ա���Է�����ʩ���˽⣬������3����Ա����1��ŮԱ���������������������ȡ2���������ڹ�˾Ⱥ���ռ�������ʩ����ǡ�ó���һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ƕ�������ͳ�ռ�������ʽ�ĸı䣬�Ƕ�����������Ч������һ�ֿ�ѧ����������Ϊ����ǿͬѧ�������������ʶ��ij�������ר������200���������з����������õ�����ͳ��ͼ���������ͳ��ͼ���ش����⣺������A���ɻ���������B������������C���к�������D��������������
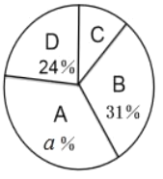
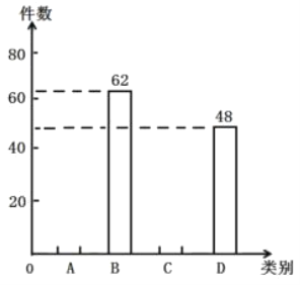
��� | ���� |
A | 70 |
B | b |
C | c |
D | 48 |
��1��![]() ________��
________��![]() ________��
________��
��2����ȫͼ�е�����ͳ��ͼ��
��3���к�����C������ͳ��ͼ����ռ��Բ�Ľ�Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���ļ�ȫ����������δ����������ˮ��ɥʧ����������ʹ�ļ��ף�����ijУΪȷ��ѧ����ȫ����չ�ˡ�Զ����ˮ���䰮�������ķ���ˮ��ȫ֪ʶ�������ִӸ�У�ߡ����꼶�и������ȡ10��ѧ���ľ����ɼ����ٷ��ƣ����������������ͷ������ɼ��÷���![]() ��ʾ�����ֳ����飺
��ʾ�����ֳ����飺![]() ��
��![]()
![]() ��
��![]() C��
C��![]() D��
D��![]() ������������˲�����Ϣ��
������������˲�����Ϣ��
���꼶10��ѧ���ľ����ɼ��ǣ�99��80��99��86��99��96��90��100��89��82
���꼶10��ѧ���ľ����ɼ���![]() ���е������ǣ�94��90��94
���е������ǣ�94��90��94
���꼶��ȡ��ѧ�������ɼ�����ͳ��ͼ��
�ߡ����꼶��ȡ��ѧ�������ɼ�ͳ�Ʊ���
�꼶 | ���꼶 | ���꼶 |
ƽ���� |
| 92 |
��� | 93 | 94 |
���� | 99 | 100 |
���� | 52 | 50.4 |
����������Ϣ������������⣺
��1��ֱ��д������ͼ����![]() ��ֵ��
��ֵ��
��2�������������ݣ�����Ϊ��У�ߡ����꼶ѧ�����շ���ˮ��ȫ֪ʶ�Ϻã���˵�����ɣ�һ�����ɼ��ɣ���
��3����У�ߡ����꼶��720�˲μ��˴˴ξ���������ƲμӴ˴ξ�����ɼ����㣨![]() ����ѧ�������Ƕ��٣�
����ѧ�������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com