
【题目】垃圾分类是对垃圾传统收集处理方式的改变,是对垃圾进行有效处理的一种科学管理方法.为了增强同学们垃圾分类的意识,某班举行了专题活动,对200件垃圾进行分类整理,得到下列统计图表,请根据统计图表回答问题:(其中A:可回收垃圾;B:厨余垃圾;C:有害垃圾;D:其它垃圾).
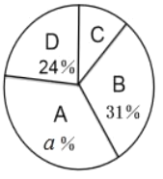
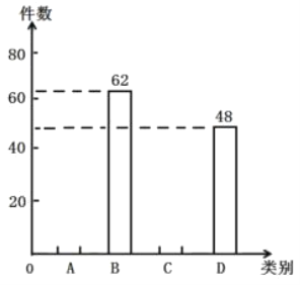
类别 | 件数 |
A | 70 |
B | b |
C | c |
D | 48 |
(1)![]() ________;
________;![]() ________;
________;
(2)补全图中的条形统计图;
(3)有害垃圾C在扇形统计图中所占的圆心角为多少?
科目:初中数学 来源: 题型:
【题目】随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽气车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元.
(1)求A、B两种型号的汽车每辆进价分别为多少方元?
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
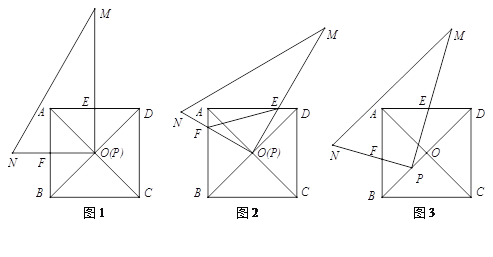
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN![]() 90°.
90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗,若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM![]() 15°时,连接EF,若正方形的边长为2,请求出线段EF的长;
15°时,连接EF,若正方形的边长为2,请求出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD![]() 3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD
3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD![]() m·BP时,请直接写出PE与PF的数量关系.
m·BP时,请直接写出PE与PF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
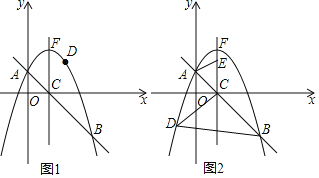
【题目】如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.
(1)求抛物线的函数表达式;
(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;
(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:如何将一个长为17,宽为1的长方形经过剪一剪,拼一拼,形成一个正方形.(下列所有图中每个小方格的边长都为1,剪拼过程中材料均无剩余)
问题探究:我们从长为5,宽为1的长方形入手.
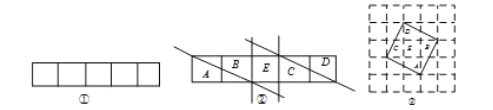
(1)如图①是一个长为5,宽为1的长方形.把这个长方形剪一剪、拼一拼后形成正方形,则正方形的面积应为_____________,设正方形的边长为![]() ,则
,则![]() _________;
_________;
(2)我们可以把有些带根号的无理数的被开方数表示成两个正整数平方和的形式,比如![]() .类比此,可以将(1)中的
.类比此,可以将(1)中的![]() 表示成
表示成![]() _____________;
_____________;
(3)![]() 的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为
的几何意义可以理解为:以长度2和3为直角边的直角三角形的斜边长为![]() ;类比此,(2)中的
;类比此,(2)中的![]() 可以理解为以长度________和__________为直角边的直角三角形斜边的长;
可以理解为以长度________和__________为直角边的直角三角形斜边的长;
(4)剪一剪:由(3)可画出如图②的分割线,把长方形分成![]() 五部分;
五部分;
(5)拼一拼:把图②中五部分拼接得到如图③的正方形;
问题解决:仿照上面的探究方法请把图④中长为17,宽为1的长方形剪一剪,在图⑤中画出拼成的正方形.(说明:图④的分割过程不作评分要求,只对图⑤中画出的最终结果评分)
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.
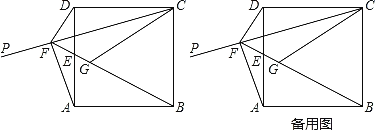
(1)试判断DF与BF的位置关系,并说明理由;
(2)若CF=4![]() ,DF=2,求AE的长;
,DF=2,求AE的长;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.

(1)、求证:BC 2=BDBA;
(2)、判断DE与⊙O位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙![]() 中,AB是直径,BC是弦,BC=BD,连接CD交⊙
中,AB是直径,BC是弦,BC=BD,连接CD交⊙![]() 于点E,∠BCD=∠DBE.
于点E,∠BCD=∠DBE.
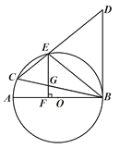
(1)求证:BD是⊙![]() 的切线.
的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=![]() ,EG=3,求BG的长.
,EG=3,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com