
【题目】如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.
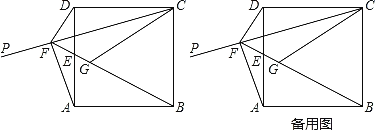
(1)试判断DF与BF的位置关系,并说明理由;
(2)若CF=4![]() ,DF=2,求AE的长;
,DF=2,求AE的长;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
【答案】(1)DF⊥BF,见解析;(2)![]() ;(3)2﹣
;(3)2﹣![]()
【解析】
(1)由轴对称的性质可得CD=CG,DF=FG,由“SSS”可证△CDF≌△CGF,可得∠CDF=∠CGF,由等腰三角形的性质和四边形内角和定理可求∠DFB=90°,可得结论;
(2)过点C作CH⊥BF于H,由等腰直角三角形的性质可求CH=FH=4,由勾股定理可求CG=BC=CD=2![]() ,通过证明△AEB∽△HBC,可得
,通过证明△AEB∽△HBC,可得![]() ,即可求解;
,即可求解;
(3)连接BD,过点F作FM⊥AD于M,作∠AFN=∠FAD,交AD于N,由题意可证点D、F、A、B四点共圆,可得∠DBF=∠DAF,∠FDA=∠FBA,可求∠FDA=30°,∠FAD=15°,利用锐角三角函数即可求解.
解:(1)DF⊥BF,
理由如下:
∵点D关于射线CP的对称点G,
∴CD=CG,DF=FG,
又∵CF=CF,
∴△CDF≌△CGF(SSS),
∴∠CDF=∠CGF,
∵CD=CB=CG,
∴∠CGB=∠CBG,
∵∠CGB+∠CGF=180°,
∴∠CBG+∠CDF=180°,
∵∠CDF+∠DFB+∠CBF+∠DCB=360°,
∴180°+90°+∠DFB=360°,
∴∠DFB=90°,
∴DF⊥BF;
(2)如图,过点C作CH⊥BF于H,
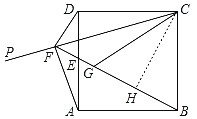
∵△CDF≌△CGF,∠DFB=90°,
∴∠CFD=∠CFG=45°,DF=FG=2,
∵CH⊥BF,
∴∠CFH=∠FCH=45°,
∴CH=FH,
∴CF=![]() CH=4
CH=4![]() ,
,
∴CH=FH=4,
∴GH=FH﹣FG=2,
∴CG![]() ,
,
∴CD=CG=BC=AB=![]() ,
,
∵CB=CG,CH⊥BG,
∴BH=GH=2,
∵AD∥BC,
∴∠AEB=∠CBH,
又∵∠DAB=∠CHB=90°,
∴△AEB∽△HBC,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ;
;
(3)连接BD,过点F作FM⊥AD于M,作∠AFN=∠FAD,交AD于N,
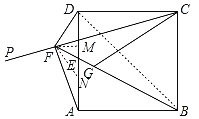
∵四边形ABCD是正方形,
∴∠ABD=∠ADB=45°,
∵∠DFB=∠DAB=90°,
∴点D、F、A、B四点共圆,
∴∠DBF=∠DAF,∠FDA=∠FBA,
∵∠ABD=∠FBD+∠FBA=∠FDA+∠DAF=45°,∠ADF=2∠FAD,
∴∠FDA=30°,∠FAD=15°,
∵∠AFN=∠FAD=15°,
∴∠FNM=30°,
又∵FM⊥AD,
∴NM=![]() FM,FN=2MF=AN,
FM,FN=2MF=AN,
∴AM=AN+MN=(2+![]() )FM,
)FM,
∴tan∠FAD=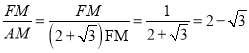 .
.


科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
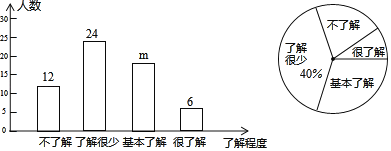
请你根据上面的信息,解答下列问题
(1)本次共调查了 名员工,条形统计图中m= ;
(2)扇形统计图中“很了解”扇形所对应的圆心角度数是_____________;
(3)若该公司共有员工1200名,请你估计不了解防护措施的人数;
(4)在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾分类是对垃圾传统收集处理方式的改变,是对垃圾进行有效处理的一种科学管理方法.为了增强同学们垃圾分类的意识,某班举行了专题活动,对200件垃圾进行分类整理,得到下列统计图表,请根据统计图表回答问题:(其中A:可回收垃圾;B:厨余垃圾;C:有害垃圾;D:其它垃圾).
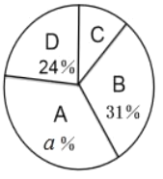
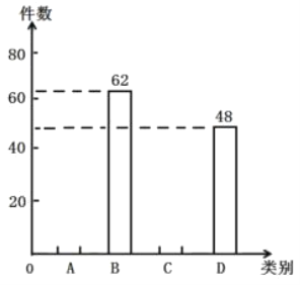
类别 | 件数 |
A | 70 |
B | b |
C | c |
D | 48 |
(1)![]() ________;
________;![]() ________;
________;
(2)补全图中的条形统计图;
(3)有害垃圾C在扇形统计图中所占的圆心角为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】110年前,中国首条自行设计和建造的铁路,京张铁路落成;110年后,在同样的地方,世界首条智能高铁京张高铁正式运行,中国速度,一直在路上,2019年底,中国高铁里程将突破3.5万公里,全世界超过![]() 的高铁轨道铺设在中国.为你骄傲,中国高铁!请将3.5万公里中的数“3.5万”用科学记数法表示为( )
的高铁轨道铺设在中国.为你骄傲,中国高铁!请将3.5万公里中的数“3.5万”用科学记数法表示为( )
A.3.5×101B.0.35×105C.35×103D.3.5×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接△ABC中,∠CAB=90°,AB=2AC,过点A作BC的垂线m交⊙O于另一点D,垂足为H,点E为![]() 上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.
(1)求证:△FED∽△AEB;
(2)若![]() =
=![]() ,AC=2,连接CE,求AE的长;
,AC=2,连接CE,求AE的长;
(3)在点E运动过程中,若BG=![]() CG,求tan∠CBF的值.
CG,求tan∠CBF的值.
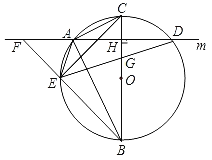
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:
表示,共分成四组:![]() .
.![]()
![]() .
.![]() C.
C.![]() D.
D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
八年级10名学生的竞赛成绩在![]() 组中的数据是:94,90,94
组中的数据是:94,90,94
八年级抽取的学生竞赛成绩扇形统计图:
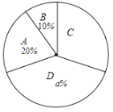
七、八年级抽取的学生竞赛成绩统计表:
年级 | 七年级 | 八年级 |
平均数 |
| 92 |
中位数 | 93 | 94 |
众数 | 99 | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中![]() 的值;
的值;
(2)根据以上数据,你认为该校七、八年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(![]() )的学生人数是多少?
)的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)求证:AG与⊙O相切.
(2)若AC=6,AB=8,BE=3,求线段OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com