
【题目】在△ABC中,点O是边AC的中点,分别过点A、C作射线BO的垂线,E、F是垂足.
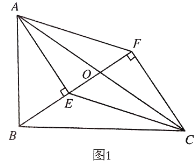
(1)如图1,求证:四边形AECF是平行四边形;
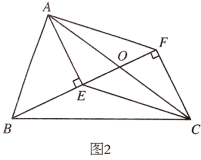
(2)如图2,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)CF=2.
【解析】
(1)根据AAS先证明△AOE≌△COF,从而得出EO=FO,结合AO=CO即可得出结论;
(2)先根据已知求出AO,CO的长,过点B作BH⊥AC于点H,在Rt△BCH中,根据![]() ,
,![]() 结合勾股定理可得出BH,CH的长,进而可求出HO的长.再在Rt△BOH中,可得出tan∠BOH=
结合勾股定理可得出BH,CH的长,进而可求出HO的长.再在Rt△BOH中,可得出tan∠BOH=![]() ,从而在Rt△AEO中,tan∠AOE=tan∠BOH=
,从而在Rt△AEO中,tan∠AOE=tan∠BOH=![]() ,结合AO的长,可以求出AE的长,由CF=AE可得出结果.
,结合AO的长,可以求出AE的长,由CF=AE可得出结果.
(1)证明:∵O为AC的中点,∴AO=CO.
又AE⊥BO,CF⊥BO,∴∠AEO=∠CFO=90°,
又∠AOE=∠FOC,∴△AOE≌△COF(AAS),
∴EO=FO,
又AO=CO,
∴四边形AECF是平行四边形;
(2)解:∵AC=BC![]() ,
,
∴AO=CO=![]() AC=
AC=![]() .
.
过点B作BH⊥AC于点H,
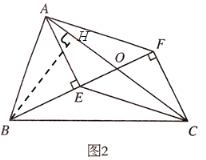
在Rt△BCH中,tan∠BCH=![]() ,
,
设BH=3x,则CH=4x,∴BC=![]() =5x=
=5x=![]() ,
,
∴x=![]() ,∴BH=
,∴BH=![]() ,CH=
,CH=![]() ,
,
∴HO=HC-OC=![]() ,
,
在Rt△BOH中,tan∠BOH=![]() ,
,
在Rt△AEO中,tan∠AOE=tan∠BOH=![]() ,
,
设OE=y,则AE=2y,AO![]() =
=![]() ,
,
∴y=1,∴AE=2,
又由(1)知四边形AECF是平行四边形,
∴CF=AE=2.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙![]() 中,AB是直径,BC是弦,BC=BD,连接CD交⊙
中,AB是直径,BC是弦,BC=BD,连接CD交⊙![]() 于点E,∠BCD=∠DBE.
于点E,∠BCD=∠DBE.
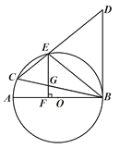
(1)求证:BD是⊙![]() 的切线.
的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=![]() ,EG=3,求BG的长.
,EG=3,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
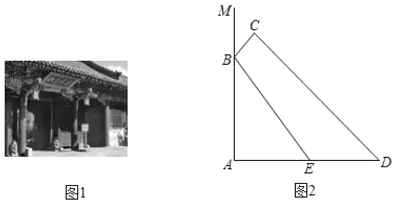
【题目】如图1,我国古建筑的大门上常常悬挂着巨大的匾额,图2中的线段![]() 就是悬挂在墙壁
就是悬挂在墙壁![]() 上的某块匾额的截面示意图.已知
上的某块匾额的截面示意图.已知![]() 米,
米,![]() .从水平地面点
.从水平地面点![]() 处看点
处看点![]() ,仰角
,仰角![]() ,从点
,从点![]() 处看点
处看点![]() ,仰角
,仰角![]() .且
.且![]() 米,求匾额悬挂的高度
米,求匾额悬挂的高度![]() 的长.(参考数据:
的长.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有5个红球、3个白球,这些球除颜色外其他都相同,在看不到球的条件下,随机地从这个袋子中摸出两个球,摸到的两个球都是红球的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
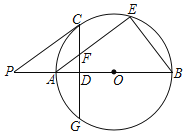
【题目】如图,AB为⊙O的直径,AE是⊙O的弦,C是弧AE的中点,弦CG⊥AB于点D,交AE于点F,过点C作⊙O的切线,交BA延长线于点P,连接BE
(1)求证:PC∥AE;
(2)若sin∠P=![]() ,CF=5,求BE的长.
,CF=5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高学生身体素质,某校决定开展足球、篮球、排球、兵乓球等四项课外体育活动,要求全员参与,并且每名学生只能选择其中一项.为了解选择各种体育活动项目的学生人数,该校随机抽取了部分学生进行调查,并绘制出如下两幅不完整的统计图,请根据统计图回答下列问题:
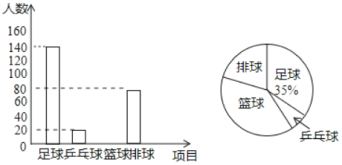
(1)直接写出这次抽样调查的学生人数;
(2)补全条形统计图;
(3)若该学校总人数是1500人,请估计选择篮球项目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
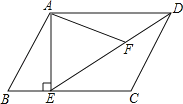
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3![]() ,AE=3,求AF的长;
,AE=3,求AF的长;
(3)若CD=CE,则直线CD是以点E为圆心,AE长为半径的圆的切线.试证明之.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com