
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且弧DE=弧BE.
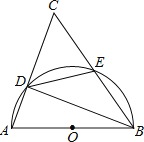
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求BD的长.
【答案】(1)△ABC为等腰三角形,理由见解析;(2)![]()
【解析】
(1)连接AE,根据圆周角定理可得∠DAE=∠BAE,∠AEB=90°,再根据相等的角的余角也相等可得∠C=∠ABC,从而得到△ABC为等腰三角形;
(2)根据“三线合一”得到BE的长,利用勾股定理求得AE的长,再利用三角形的面积公式即可求得BD的长.
解:(1)△ABC为等腰三角形.
理由如下:连结AE,如图,
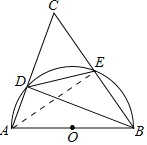
∵![]() ,
,
∴∠DAE=∠BAE,即AE平分∠BAC,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∵∠C+∠CAE=90°,∠ABC+∠BAE=90°,
∴∠C=∠ABC,
∴AC=AB,
∴△ABC为等腰三角形;
(2)∵△ABC为等腰三角形,AE⊥BC,
∴,![]() ,
,
在Rt△ABE中,
∵AB=10,BE=6,
∴![]() ,
,
∵AB为直径,
∴∠ADB=90°,
∴![]() ,
,
∴![]() .
.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
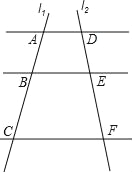
【题目】如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,![]() ,AC=14;
,AC=14;
(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
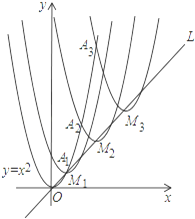
【题目】如图,抛物线y=x2在第一象限内经过的整数点(横坐标,纵坐标都为整数的点)依次为A1,A2,A3,…An,…,将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,….
则M2016顶点的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2﹣1)=80,试求2m2+n2的值
解:设2m2+n2=t,则原方程变为(t+1)(t﹣1)=80,整理得t2﹣1=80,t2=81,∴t=±9因为2m2+n2≥0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
已知实数x,y满足(4x2+4y2+3)(4x2+4y2﹣3)=27,求x2+y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
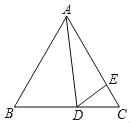
【题目】如图,等边△ABC中,D为BC边上一点,E为AC边上一点,∠ADE=60°
(1)求证:△ABD∽△DCE;
(2)若BD=4,CE=![]() ,求△ABC的边长.
,求△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19m),另外三边利用学校现有总长38m的铁栏围成.
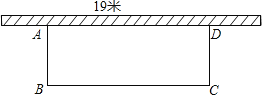
(1)若围成的面积为180m,试求出自行车车棚的长和宽;
(2)能围成的面积为200m自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
①4ac<b2;
②a>b>c;
③一次函数y=ax+c的图象不经第四象限;
④m(am+b)+b<a(m是任意实数);
⑤3b+2c>0.
其中正确的个数是( )
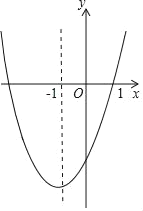
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副三角板的三个内角分别是90°,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上),若固定△ABC,将△BDE绕着公共顶点B顺时针旋转α度(0<α<180),当边DE与△ABC的某一边平行时,相应的旋转角α的值为____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com