
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
①4ac<b2;
②a>b>c;
③一次函数y=ax+c的图象不经第四象限;
④m(am+b)+b<a(m是任意实数);
⑤3b+2c>0.
其中正确的个数是( )
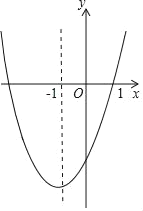
A.1B.2C.3D.4
【答案】A
【解析】
利用抛物线与x轴交点个数可对①进行判断;利用抛物线开口方向得到a>0,利用抛物线的对称轴方程得到b=2a>0,利用抛物线与y轴的交点位置得到c<0,则可对②进行判断;根据一次函数的性质可对③进行判断;根据当x=﹣1时,二次函数有最小值,可对④进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点坐标,利用a![]() b得到3b+2c=0,则可对⑤进行判断.
b得到3b+2c=0,则可对⑤进行判断.
∵抛物线与x轴有两个交点,∴b2﹣4ac>0,即4ac<b2,∴①正确;
∵抛物线开口向上,∴a>0.
∵抛物线的对称轴为直线x![]() 1,∴b=2a>0.
1,∴b=2a>0.
∵抛物线与y轴的交点在x轴下方,∴c<0,∴b>a>c,∴②错误;
∵a>0,c<0,∴一次函数y=ax+c的图象经过一三四象限,不过第二象限,∴③错误;
∵抛物线的对称轴为直线x=﹣1,∴当x=﹣1时,函数有最小值y=a﹣b+c,∴am2+bm+c≥a﹣b+c,即m(am+b)+b≥a,∴④错误;
∵抛物线与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,∴抛物线与x轴的另一个交点坐标为(﹣3,0),∴9a﹣3b+c=0,∴18a﹣6b+2c=0.
∵b=2a,则a![]() b,∴9b﹣6b+2c=0,即3b+2c=0,∴⑤错误.
b,∴9b﹣6b+2c=0,即3b+2c=0,∴⑤错误.
故选A.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过点
过点![]() ,
,![]() ,过定点
,过定点![]() 的直线
的直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
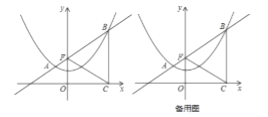
(1)求抛物线的解析式;
(2)当点![]() 在抛物线上运动时,判断线段
在抛物线上运动时,判断线段![]() 与
与![]() 的数量关系(
的数量关系(![]() 、
、![]() 、
、![]() ),并证明你的判断;
),并证明你的判断;
(3)![]() 为
为![]() 轴上一点,以
轴上一点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,设点
为顶点的四边形是菱形,设点![]() ,求自然数
,求自然数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且弧DE=弧BE.
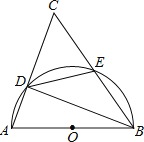
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时, ![]() ?
? ![]() 当x取什么值时,y的值随x的增大而减小?
当x取什么值时,y的值随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
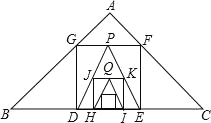
【题目】如图,已知在Rt△ABC中,AB=AC=3![]() ,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=70°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
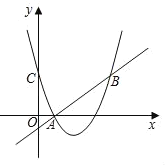
【题目】如图,二次函数y=(x﹣3)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)抛物线上是否存在一点P,使S△ABP=S△ABC?若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com