
| BF |
| CF |
| DN |
| CN |

| AM |
| AF |
| DM |
| BF |
| AM |
| AF |
| EM |
| CF |
| DM |
| BF |
| EM |
| CF |
| DM |
| ME |
| BF |
| CF |
| DM |
| ME |
| DN |
| CN |
| BF |
| CF |
| DN |
| CN |
| BD |
| AB |
| BF |
| BC |
| 5-t |
| 5 |
| t |
| 6 |
| 30 |
| 11 |
| AD |
| AB |
| DE |
| BC |
| BF |
| AB |
| DB |
| BC |
| AM |
| AF |
| DM |
| BF |
| AM |
| AF |
| EM |
| CF |
| DM |
| BF |
| EM |
| CF |
| DM |
| ME |
| BF |
| CF |
| DM |
| ME |
| DN |
| CN |
| BF |
| CF |
| DN |
| CN |
| 10 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
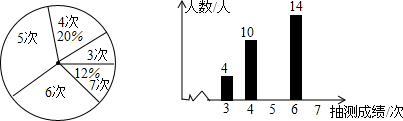
| A、4.2 | B、4.68 |
| C、5 | D、5.16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
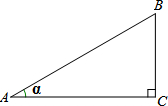 如图,定义:在Rt△ABC中,∠C=90°,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=
如图,定义:在Rt△ABC中,∠C=90°,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=| 角α的邻边 |
| 角α的对边 |
| AC |
| BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
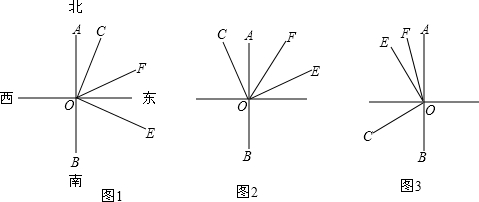
查看答案和解析>>
科目:初中数学 来源: 题型:
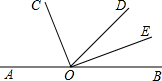 如果,O是直线AB上的一点,射线OC、OE分别平分∠AOD和∠BOD.
如果,O是直线AB上的一点,射线OC、OE分别平分∠AOD和∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:
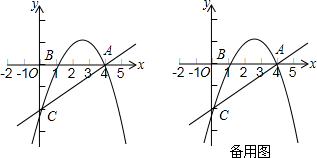
查看答案和解析>>
科目:初中数学 来源: 题型:
| 销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com