Question

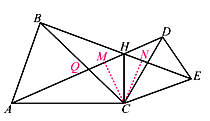
【题目】如图，CA＝CB，CD＝CE，∠ACB＝∠DCE＝α，AD、BE交于点H，连接CH.

(1)求证：△ACD≌△BCE；

(2)求证：CH平分∠AHE；

(3)求∠CHE的度数．(用含α的式子表示)

Answer 1

【答案】(1)证明见解析；(2) 证明见解析；(3) 90°－α

【解析】试题分析：（1）由CA=CB，CD=CE，∠ACB=∠DCE=α，利用SAS，即可判定：△ACD≌△BCE；
（2）首先作CM⊥AD于M，CN⊥BE于N，由△ACD≌△BCE，可证∠CAD=∠CBE，再证△ACM≌△BCN，（或证△ECN≌△DCM），可得CM=CN，即可证得CH平分∠AHE；
（3）由△ACD≌△BCE，可得∠CAD=∠CBE，继而求得∠AHB=∠ACB=α，则可求得∠CHE的度数．

试题解析：(1)证明：∵∠ACB＝∠DCE＝α，

∴∠ACD＝∠BCE.

在△ACD和△BCE中，

∴△ACD≌△BCE(SAS)．

(2)证明：过点C作CM⊥AD于M，CN⊥BE于N.

∵△ACD≌△BCE，∴∠CAM＝∠CBN.

在△ACM和△BCN中，

∴△ACM≌△BCN.

∴CM＝CN.

∴CH平分∠AHE.

(3)令BC、AH交于点Q.

∵∠AQC＝∠BQH，∠CAD＝∠CBE，

∴∠AHB＝∠ACB＝α.

∴∠AHE＝180°－α.

∴∠CHE＝∠AHE＝90°－α.