
【题目】探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?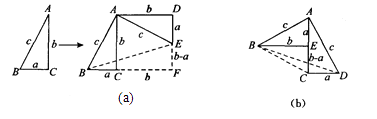
【答案】解:方法1:∵由图(a)可知S正方形ACFD=S四边形ABFE ,
∴S正方形ACFD=S⊿BAE+S⊿BFE
又∵正方形ACFD的边长为b, SRt△BAE= ![]() ,SRt△BFE=
,SRt△BFE= ![]()
∴b2 = ![]() +
+ ![]()
即2b2 =c2 +(b+a)(b-a)
整理得: a2 +b2=c2
方法2:如图(b)中,Rt△BEA和Rt△ACD全等, 设CD=a,AC=b,AD=c(b>a),
则AE=a,BE=b,AB=c,EC=b-a
由图(b),S四边形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD
又∵ SRt△BAE = ![]() , SRt△ACD =
, SRt△ACD = ![]() ,SRt△BEC =
,SRt△BEC = ![]() ,
,
SRt△BAD= ![]() ,S△BCD=
,S△BCD= ![]() ,
,
∴ ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]()
即2ab+b(b-a) = c2 +a(b-a)
整理得: a2 +b2=c2
【解析】方法1:由S正方形ACFD=S⊿BAE+S⊿BFE,从而列出方程进行解答即可;
(2)方法2:由S四边形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD,列方程解答即可。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.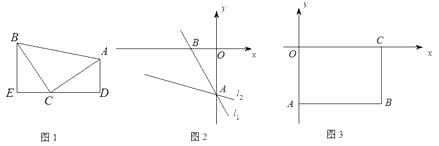
(1)求证:△BEC≌△CDA;
(2)模型应用:
①已知直线l1:y=- ![]() x-4与y轴交于A点,将直线l1绕着A点逆时针旋转45°至l2 , 如图2,求l2的函数解析式;
x-4与y轴交于A点,将直线l1绕着A点逆时针旋转45°至l2 , 如图2,求l2的函数解析式;
②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,-6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第四象限,且是直线y=-2x+6上的一点,若△APD是不以点A为直角顶点的等腰Rt△,请求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.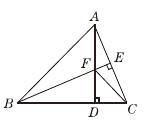
(1)求证:BF=2AE;
(2)若CD= ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com