
【题目】对于一个关于x的代数式A,若存在一个系数为正数关于x的单项式F,使![]() 的结果是所有系数均为整数的整式,则称单项式F为代数式A的“整系单项式”.例如:
的结果是所有系数均为整数的整式,则称单项式F为代数式A的“整系单项式”.例如:
当A=![]() ,F=2x3时,由于
,F=2x3时,由于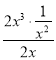 =1,故2x3是
=1,故2x3是![]() 的整系单项式;
的整系单项式;
当A=![]() ,F=6x5时,由于
,F=6x5时,由于 ,故6x5是
,故6x5是![]() 的整系单项式;
的整系单项式;
当A=3-![]() ,F=
,F=![]() 时,由于
时,由于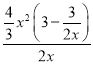 =2x-1,故
=2x-1,故![]() 是3-
是3-![]() 的整系单项式;
的整系单项式;
当A=3-![]() ,F=8x4时,由于
,F=8x4时,由于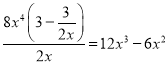 ,故8x4是3-
,故8x4是3-![]() 的整系单项式;
的整系单项式;
显然,当代数式A存在整系单项式F时,F有无数个,现把次数最低,系数最小的整系单项式F记为F(A).例如:![]() ,
,![]()
阅读以上材料并解决下列问题:
(1)判断:当A=![]() 时,F=2x3______A的整系单项式(填“是”或“不是”)
时,F=2x3______A的整系单项式(填“是”或“不是”)
(2)解方程: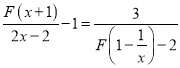
(3)已知a、b、c是△ABC的边长,其中a、b满足(a-5)2+![]() =0,且关于x的方程|
=0,且关于x的方程|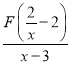 |=c有且只有3个不相等的实数根,求△ABC的周长.
|=c有且只有3个不相等的实数根,求△ABC的周长.
【答案】(1)是;(2)x=![]() ;(3)26或27;
;(3)26或27;
【解析】
(1)当A=![]() 时,F=2x3时,
时,F=2x3时,![]() =x;
=x;
(2)令F=axn,结合定义进行判断,即可求出F(x+1)=2x,F(1-![]() )=2x2,将所求方程转化为
)=2x2,将所求方程转化为![]() -1=
-1=![]() 即可求解;
即可求解;
(3)根据平方与二次根式的性质可求a=5,b=9,再求出F(![]() )=x2,将所求式子转化为可以化为|
)=x2,将所求式子转化为可以化为|![]() |=c,结合函数图象即可求解;
|=c,结合函数图象即可求解;
解:(1)当A=![]() 时,F=2x3时,
时,F=2x3时,![]() =x,
=x,
∴![]() 是2x3的整系单项式;
是2x3的整系单项式;
(2)F(x+1)=2x,F(1-![]() )=2x2,
)=2x2,
∴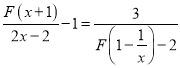 可以化为
可以化为![]() -1=
-1=![]() ,
,
∴2x2-3x+1=0,
∴x=1或x=![]() ;
;
经检验x=1是方程的增根,
∴原方程的解为x=![]() ;
;
(3)∵(a-5)2+![]() =0,
=0,
∴a=5,b=9,
F(![]() )=x2,
)=x2,
∴|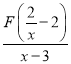 |=c可以化为|
|=c可以化为|![]() |=c,
|=c,
∴|(x-3)+![]() +6|=c,
+6|=c,
当x=6时,c=12,
∴当x≥6时,c≥12,此时方程有且只有3个不相等的实数根,
∵c<14,
∴c=12或c=13,
∴△ABC的周长为26或27;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
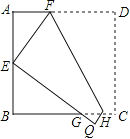
【题目】如图,将边长为6的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,点D, E, F分别是AB,AC, BC的中点,连接DE,DF.
(1)求证:四边形DFCE是菱形;
(2)若∠A=75°,AC=4,求菱形DFCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“学习朱子文化,弘扬理学思想”为主题的读书月活动,并向学生征集读后感,学校将收到的读后感篇数按年级进行统计,绘制了以下两幅统计图(不完整).
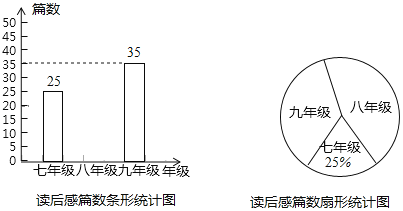
据图中提供的信息完成以下问题
(1)扇形统计图中“八年级”对应的圆心角是 °,并补全条形统计图;
(2)经过评审,全校有4篇读后感荣获特等奖,其中有一篇来自七年级,学校准备从特等奖读后感中任选两篇在校广播电台上播出,请利用画树状图或列表的方法求出七年级特等奖读后感被校广播电台播出的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初2019级即将迎来中考,很多家长都在为孩子准备营养午餐.一家快餐店看准了商机,在5月5号推出了A,B,C三种营养套餐.套餐C单价比套餐A贵5元,三种套餐的单价均为整数,其中A套餐比C套餐少卖12份,B套餐比C套餐少卖6份,且C套餐当天卖出的数量大于26且不超过32,当天总销售量为偶数且当天销售额达到了1830元,商家发现C套餐很受欢迎,因此在6号加推出了C套餐升级版D套餐,四种套餐同时售卖,A套餐比5号销售量减少,C套餐比5号销售量增加![]() ,且A减少的份数比C套餐增加的份数多5份,B套餐销售量不变,由于商家人手限制,两天的总销售量相同,则其他套餐单价不变的情况下,D套餐至少比C套餐费贵______时,才能使6号销售额达到1950元.
,且A减少的份数比C套餐增加的份数多5份,B套餐销售量不变,由于商家人手限制,两天的总销售量相同,则其他套餐单价不变的情况下,D套餐至少比C套餐费贵______时,才能使6号销售额达到1950元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同的路线从A地到B地,所行驶的路程与时间的函数图形如图所示,下列说法正确的有( )
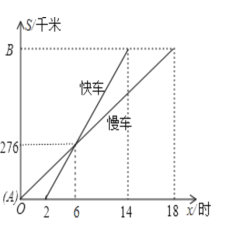
①快车追上慢车需6小时;②慢车比快车早出发2小时;③快车速度为46km/h;④慢车速度为46km/h; ⑤A、B两地相距828km;⑥快车从A地出发到B地用了14小时
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
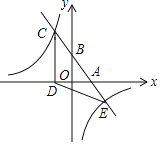
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )
A. a≤﹣1或![]() ≤a<
≤a<![]() B.
B. ![]() ≤a<
≤a<![]()
C. a≤![]() 或a>
或a>![]() D. a≤﹣1或a≥
D. a≤﹣1或a≥![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com