
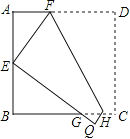
【题目】如图,将边长为6的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在点Q处,EQ与BC交于点G,则△EBG的周长是 cm.
【答案】12
【解析】
试题根据翻折的性质可得DF=EF,设EF=x,表示出AF,然后利用勾股定理列方程求出x,从而得到AF、EF的长,再求出△AEF和△BGE相似,根据相似三角形对应边成比例列式求出BG、EG,然后根据三角形周长的定义列式计算即可得解.
解:由翻折的性质得,DF=EF,
设EF=x,则AF=6﹣x,
∵点E是AB的中点,
∴AE=BE=![]() ×6=3,
×6=3,
在Rt△AEF中,AE2+AF2=EF2,
即32+(6﹣x)2=x2,
解得x=![]() ,
,
∴AF=6﹣![]() =
=![]() ,
,
∵∠FEG=∠D=90°,
∴∠AEF+∠BEG=90°,
∵∠AEF+∠AFE=90°,
∴∠AFE=∠BEG,
又∵∠A=∠B=90°,
∴△AEF∽△BGE,
∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() =
=![]() ,
,
解得BG=4,EG=5,
∴△EBG的周长=3+4+5=12.
故答案为12.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
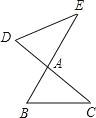
【题目】如图,BE、CD 相交于点 A,连接 BC,DE,下列条件中不能判断△ABC∽ADE 的是( )
A. ∠B=∠D B. ∠C=∠E C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
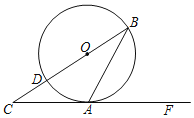
【题目】如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线CF交BD延长线于点C.
(Ⅰ)若∠C=25°,求∠BAF的度数;
(Ⅱ)若AB=AC,CD=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() ,
,![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,且交
的直径,且交![]() 于点
于点![]() .
.
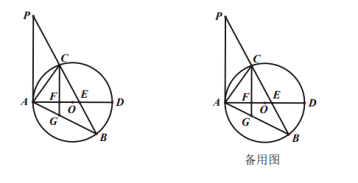
(1)求证: ![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() 若
若![]() 求
求![]() 的长;
的长;
(3)在满足(2)的条件下,若![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m2﹣1与y轴交于点C.
(1)试用含m的代数式表示抛物线的顶点坐标;
(2)将抛物线y=x2﹣2mx+m2﹣1沿直线y=﹣1翻折,得到的新抛物线与y轴交于点D.若m>0,CD=8,求m的值;
(3)已知A(2k,0),B(0,k),在(2)的条件下,当线段AB与抛物线y=x2﹣2mx+m2﹣1只有一个公共点时,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将抛物线![]() (m≠0)向右平移
(m≠0)向右平移![]() 个单位长度后得到抛物线G2,点A是抛物线G2的顶点.
个单位长度后得到抛物线G2,点A是抛物线G2的顶点.
(1)直接写出点A的坐标;
(2)过点(0,![]() )且平行于x轴的直线l与抛物线G2交于B,C两点.
)且平行于x轴的直线l与抛物线G2交于B,C两点.
①当∠BAC=90°时.求抛物线G2的表达式;
②若60°<∠BAC<120°,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个关于x的代数式A,若存在一个系数为正数关于x的单项式F,使![]() 的结果是所有系数均为整数的整式,则称单项式F为代数式A的“整系单项式”.例如:
的结果是所有系数均为整数的整式,则称单项式F为代数式A的“整系单项式”.例如:
当A=![]() ,F=2x3时,由于
,F=2x3时,由于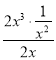 =1,故2x3是
=1,故2x3是![]() 的整系单项式;
的整系单项式;
当A=![]() ,F=6x5时,由于
,F=6x5时,由于 ,故6x5是
,故6x5是![]() 的整系单项式;
的整系单项式;
当A=3-![]() ,F=
,F=![]() 时,由于
时,由于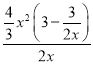 =2x-1,故
=2x-1,故![]() 是3-
是3-![]() 的整系单项式;
的整系单项式;
当A=3-![]() ,F=8x4时,由于
,F=8x4时,由于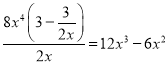 ,故8x4是3-
,故8x4是3-![]() 的整系单项式;
的整系单项式;
显然,当代数式A存在整系单项式F时,F有无数个,现把次数最低,系数最小的整系单项式F记为F(A).例如:![]() ,
,![]()
阅读以上材料并解决下列问题:
(1)判断:当A=![]() 时,F=2x3______A的整系单项式(填“是”或“不是”)
时,F=2x3______A的整系单项式(填“是”或“不是”)
(2)解方程: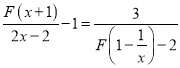
(3)已知a、b、c是△ABC的边长,其中a、b满足(a-5)2+![]() =0,且关于x的方程|
=0,且关于x的方程|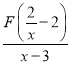 |=c有且只有3个不相等的实数根,求△ABC的周长.
|=c有且只有3个不相等的实数根,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com