
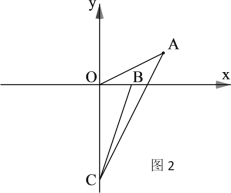
【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的BC方向移动,距台风中心500km的范围是受台风影响的区域
(1)A城是否受这次台风的影响?
(2)若A城受到这次台风的影响,那么A城遭受台风影响有多长时间?

【答案】(1)受影响;(2)4小时
【解析】
(1)点到直线的线段中垂线段最短,故应由A点向BC作垂线,垂足为M,若AM>500则A城不受影响,否则受影响;
(2)点A到直线BC的长为500千米的点有两点,分别设为D、G,则△ADG是等腰三角形,由于AM⊥BC,则M是DG的中点,在Rt△ADM中,解出MD的长,则可求DG长,在DG长的范围内都是受台风影响,再根据速度与距离的关系则可求时间.
(1)(1)A城受到这次台风的影响,
理由:由A点向BC作垂线,垂足为M,
在Rt△ABM中,∠ABM=30°,AB=600km,则AM=300km,
因为300<500,所以A城要受台风影响;
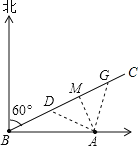
(2)设BC上点D,DA=500千米,则还有一点G,有
AG=500千米.
因为DA=AG,所以△ADG是等腰三角形,
因为AM⊥BC,所以AM是DG的垂直平分线,MD=GM,
在Rt△ADM中,DA=500千米,AM=300千米,
由勾股定理得,MD=![]() =
=![]() =400(千米),
=400(千米),
则DG=2DM=800千米,
遭受台风影响的时间是:t=800÷200=4(小时),
答:A城遭受这次台风影响时间为4小时.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】用1块A型钢板可制成2块C型钢板,1块D型钢板,用1块B型钢板可制成1块C型钢板,2块D型钢板.
(1)现需要15块C型钢板,18块D型钢板,可恰好用A型钢板,B型钢板各多少块?
(2)若购买A型钢板和B型钢板共20块.要求制成C型钢板不少于25块,D型钢板不少于30块,求A、B型钢板的购买方案共有多少种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
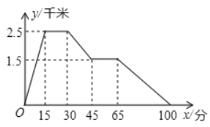
【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
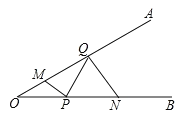
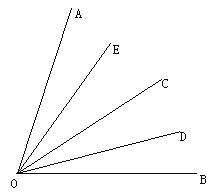
【题目】如图,∠AOB=30°,M、N分别在OA、OB上,且OM=2,ON=4,点P、Q分别在OB、OA上,则MP+PQ+QN的最小值是 _______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知A(a,b),且a.b满足![]() ,
,
(1)求A点的坐标及线段OA的长度;(2)点P为x轴正半轴上一点,且△AOP是等腰三角形,求P点的坐标;
(3)如图2,若B(1,0),C(0,-3),试确定∠ACO+∠BCO的值是否发生变化,若不变,求其值;若变化,请求出变化范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=80°,如图,OC是∠AOB的平分线,OD、OE分别平分∠BOC和∠AOC,
(1)求∠DOE的度数;
(2)当OC在∠AOB内绕O点旋转时,OD、OE仍是∠BOC和∠AOC的平分线,问此时∠DOE的大小是否和(1)中的答案相同?通过此过程,你能总结出怎样的结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了了解七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查。根据收集的数据绘制了下面的频数分市直方图,则以下说法正确的是( )

A. 绘制该频数分布直方图时选取的组距为10分成的组数为5
B. 这50人中大多数学生参加社会实践活动的时间是12-14h
C. 这50人中有64%的学生参加社会实践活动时间不少于10h
D. 可以估计全年级700人中参加社会实践活动时间为6~8h的学生大约为28人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.
与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.

(1)求S△ABD的值;
(2)如图2,若点P是直线AD下方抛物线上一动点,过点P作PF∥y轴交直线AD于点F,作PG∥AC交直线AD于点G,当△PGF的周长最大时,在线段DE上取一点Q,当PQ+![]() QE的值最小时,求此时PQ+
QE的值最小时,求此时PQ+ ![]() QE的值;
QE的值;
(3)如图3,M是BC的中点,以CM为斜边作直角△CMN,使CN∥x轴,MN∥y轴,将△CMN沿射线CB平移,记平移后的三角形为△C′M′N′,当点N′落在x轴上即停止运动,将此时的△C′M′N′绕点C′逆时针旋转(旋转度数不超过180°),旋转过程中直线M′N′与直线CA交于点S,与y轴交于点T,与x轴交于点W,请问△CST是否能为等腰三角形?若能,请求出所有符合条件的WN′的长度;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com