
【题目】已知∠AOB=80°,如图,OC是∠AOB的平分线,OD、OE分别平分∠BOC和∠AOC,
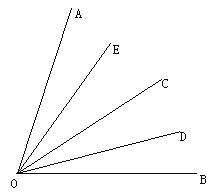
(1)求∠DOE的度数;
(2)当OC在∠AOB内绕O点旋转时,OD、OE仍是∠BOC和∠AOC的平分线,问此时∠DOE的大小是否和(1)中的答案相同?通过此过程,你能总结出怎样的结论?
【答案】(1)∠DOE=40°;(2)∠DOE大小不变,结论:OC不论怎样变化,只要∠AOB不变,总有∠DOE=∠AOB.
【解析】
(1)根据角平分线的定义求得∠AOC=∠BOD=![]() ∠AOB=
∠AOB=![]() ×80°=40,再由角平分线的定义求得,∠DOC=
×80°=40,再由角平分线的定义求得,∠DOC=![]() ∠BOC=
∠BOC=![]() ×40°=20°,∠EOC=
×40°=20°,∠EOC=![]() ∠AOC=
∠AOC=![]() ×40°=20°,即可求解;
×40°=20°,即可求解;
(2)根据角平分线的定义求得,∠DOE=∠DOC+∠EOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB,从而解决问题.
∠AOB,从而解决问题.
解:(1)∵OC是∠AOB的平分线 ,
∴∠AOC=∠BOD=![]() ∠AOB=
∠AOB=![]() ×80°=40°,
×80°=40°,
∵OD、OE分别平分∠BOC、∠AOC ,
∴∠DOC=![]() ∠BOC=
∠BOC=![]() ×40°=20°,
×40°=20°,
∠EOC=![]() ∠AOC=
∠AOC=![]() ×40°=20°,
×40°=20°,
∴∠DOE=∠DOC=∠EOC=20°+20°=40°.
(2)当OC旋转时,
∵OD、OE仍为∠BOC、∠AOC的平分线,
∴∠DOC=![]() ∠BOC,∠EOC=
∠BOC,∠EOC=![]() ∠AOC,
∠AOC,
∴∠DOE=∠DOC+∠EOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=
∠AOB=![]() ×80°=40°,
×80°=40°,
∴∠DOE大小不变,
∴OC不论怎样变化,只要∠AOB不变,总有∠DOE=∠AOB.


科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的BC方向移动,距台风中心500km的范围是受台风影响的区域
(1)A城是否受这次台风的影响?
(2)若A城受到这次台风的影响,那么A城遭受台风影响有多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
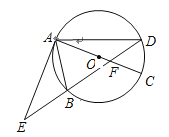
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点(0,2)和点(1,﹣1).
(1)求这个一次函数的解析式;
(2)求此一次函数图象与两坐标轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1的正方形,已知学校的坐标为A(2,2).
(1)请在图中建立适当的直角坐标系,并写出图书馆的坐标;
(2)若体育馆的坐标为C(-2,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com