
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,斜率为k(k≠0)的直线l过点(1,0),且与椭圆C相交于不同的两点A,B.
,过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,斜率为k(k≠0)的直线l过点(1,0),且与椭圆C相交于不同的两点A,B.
(Ⅰ)求椭圆C的方程;
(Ⅱ)在x轴上是否存在点M,使得无论k取何值, ![]() 为定值?若存在,求出点M的坐标;若不存在,请说明理由.
为定值?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】解:(I)由过左焦点F且垂直于x轴的直线与椭圆C相交,所得弦长为1,
可知椭圆C过点 ![]() ,∴
,∴ ![]() ,
,
又∵e= ![]() =
= ![]() ,a2=b2+c2;
,a2=b2+c2;
三式联立解得 ![]() ,
,
∴椭圆的方程为 ![]() +y2=1;…(4分)
+y2=1;…(4分)
(II)设在x轴上存在点M(t,0)满足题意,
∵直线l过点(1,0)且斜率为k,则直线l的方程可设为:y=k(x﹣1);
由 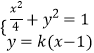 可知:x2+4k2(x﹣1)2=4,
可知:x2+4k2(x﹣1)2=4,
整理得(1+4k2)x2﹣8k2x+4k2﹣4=0;
易知:△=64k4﹣16(1+4k2)(k2﹣1)=16(3k2+1)>0;
设 A(x1 , y1),B(x2 , y2),
则:  ;
;
∴ ![]()
![]() =(x1﹣t,y1)(x2﹣t,y2)
=(x1﹣t,y1)(x2﹣t,y2)
=(x1﹣t)(x2﹣t)+y1y2
=x1x2﹣t(x1+x2)+t2+k2(x1﹣1)(x2﹣1)
=(1+k2)x1x2﹣(t+k2)(x1+x2)+t2+k2
= ![]() ;
;
由题意可设: ![]()
![]() ﹣
﹣ ![]() =m(m为常数),
=m(m为常数),
∴k2(4t2﹣8t)+t2﹣4=m+4mk2对任意实数k(k≠0)恒成立;
∴ ![]() ,解得:t=2,m=0;
,解得:t=2,m=0;
∴存在点M(2,0)满足题意,且常数为0.
【解析】(I)由题意知椭圆C过点 ![]() ,代入椭圆方程,再由离心率e以及a、b、c的关系列方程组求出a、b即可;(II)设在x轴上存在点M(t,0)满足题意,设出直线l的方程,与椭圆方程联立消去y,利用根与系数的关系得出x1+x2与x1x2 , 其中A(x1 , y1),B(x2 , y2);再计算
,代入椭圆方程,再由离心率e以及a、b、c的关系列方程组求出a、b即可;(II)设在x轴上存在点M(t,0)满足题意,设出直线l的方程,与椭圆方程联立消去y,利用根与系数的关系得出x1+x2与x1x2 , 其中A(x1 , y1),B(x2 , y2);再计算 ![]()
![]() ﹣
﹣ ![]() 的值,即可求出结论.
的值,即可求出结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( ) 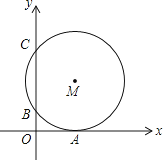
A.10
B.8 ![]()
C.4 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三棱锥ABC﹣A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2 ![]() .
. 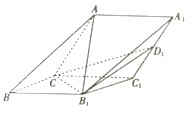
(1)求证:AB1⊥CC1;
(2)若AB1=3 ![]() ,D1为线段A1C1上的点,且三棱锥C﹣B1C1D1的体积为
,D1为线段A1C1上的点,且三棱锥C﹣B1C1D1的体积为 ![]() ,求
,求 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() .(a为常数,a>0) (Ⅰ)若
.(a为常数,a>0) (Ⅰ)若 ![]() 是函数f(x)的一个极值点,求a的值;
是函数f(x)的一个极值点,求a的值;
(Ⅱ)求证:当0<a≤2时,f(x)在 ![]() 上是增函数;
上是增函数;
(Ⅲ)若对任意的a∈(1,2),总存在 ![]() ,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f(x0)=3,x0∈( ![]() ,
, ![]() ),则sinx0的值为( )
),则sinx0的值为( ) 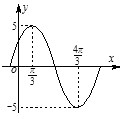
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B分别在射线CM、CN(不含端点C)上运动,∠MCN= ![]() π,在△ABC中,角A、B、C所对的边分别是a、b、c.
π,在△ABC中,角A、B、C所对的边分别是a、b、c. 
(Ⅰ)若a、b、c依次成等差数列,且公差为2.求c的值;
(Ⅱ)若c= ![]() ,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据某市地产数据研究院的数据显示,2016年该市新建住宅销售均价走势如图所示,为抑制房价过快上涨,政府从8月份采取宏观调控措施,10月份开始房价得到很好的抑制. 
(Ⅰ)地产数据研究院研究发现,3月至7月的各月均价y(万元/平方米)与月份x之间具有较强的线性相关关系,试建立y关于x的回归方程(系数精确到0.01),政府若不调控,依次相关关系预测第12月份该市新建住宅销售均价;
(Ⅱ)地产数据研究院在2016年的12个月份中,随机抽取三个月份的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为X,求X的分布列和数学期望.
参考数据: ![]() =25,
=25, ![]() =5.36,
=5.36, ![]() =0.64
=0.64
回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆 ![]() 为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为
为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为 ![]() .
.
(1)求线段AD的中点M的轨迹E的普通方程;
(2)利用椭圆C的极坐标方程证明 ![]() 为定值,并求△AOB的面积的最大值.
为定值,并求△AOB的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com