【题目】已知椭圆 为参数），A，B是C上的动点，且满足OA⊥OB（O为坐标原点），以原点O为极点，x轴的正半轴为极轴建立坐标系，点D的极坐标为 ．
（1）求线段AD的中点M的轨迹E的普通方程；
（2）利用椭圆C的极坐标方程证明 为定值，并求△AOB的面积的最大值．

参考答案：

【答案】
（1）解：点D的直角坐标为 ，由题意可设点A的坐标为（2cosα，sinα）参数，

则线段AD的中点M的坐标为 ，

所以点M的轨迹E的参数方程为 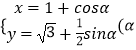为参数）

消去α可得E的普通方程为


（2）解：椭圆C的普通方程为 ，化为极坐标方程得ρ2+3ρ2sin2θ=4，

变形得 ，

由OA⊥OB，不妨设 ，所以

= （定值），

S△AOB= ρ1ρ2= = ，

易知当sin2θ=0时，S取得最大值1


【解析】（1）由题意求得线段AD中点坐标M，即可求得M的轨迹E的参数方程，消去α，即可求得E的普通方程；（2）由椭圆的普通方程，求得极坐标方程，求得 ，由OA⊥OB，根据 ，化简即可求得 = 为定值，根据三角形的面积公式，利用二倍角公式，及三角函数的性质，即可求得△AOB面积的最大值．

关闭