练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P．若点P的坐标为（2a，b+1），则a与b的数量关系为（　）

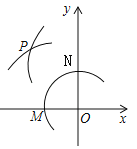
    A. a=b B. 2a﹣b=1 C. 2a+b=﹣1 D. 2a+b=1

    【答案】B

    【解析】试题分析：根据作图过程可得P在第二象限角平分线上，有角平分线的性质：角的平分线上的点到角的两边的距离相等可得|2a|=|b+1|，再根据P点所在象限可得横纵坐标的和为0，进而得到a与b的数量关系．

    解：根据作图方法可得点P在第二象限角平分线上，

    则P点横纵坐标的和为0，

    故2a+b+1=0，

    整理得：2a+b=﹣1，

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一个圆绕它的直径旋转一周形成的几何体是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y＝x2－2mx＋4m－8的顶点为A

    (1) 求证：该抛物线与x轴总有两个交点

    (2) 当m＝1时，直线BC：y＝kx－2与该抛物线交于B、C两点，若线段BC被x轴平分，求k的值

    (3) 以A为一个顶点作该抛物线的内接正三角形AMN（M、N两点在抛物线上），请问：△AMN的面积是与m无关的定值吗？若是，请求出这个定值；若不是，请说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列哪一种正多边形不能铺满地面（ ）

    A. 正三边形B. 正四边形C. 正六边形D. 正八边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】[6a2b2+___+____]÷2ab2=3a+b-1.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：关于x的二次函数y=x2+bx+c经过点（﹣1，0）和（2，6）．

    （1）求b和c的值．

    （2）若点A（n，y1），B（n+1，y2），C（n+2，y3）都在这个二次函数的图象上，问是否存在整数n，使？若存在，请求出n；若不存在，请说明理由．

    （3）若点P是二次函数图象在y轴左侧部分上的一个动点，将直线y=﹣2x沿y轴向下平移，分别交x轴、y轴于C、D两点，若以CD为直角边的△PCD与△OCD相似，请求出所有符合条件点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2013年12月15日，我国“玉兔号”月球车顺利抵达月球表面，月球离地球平均距离是384 400 000米，数据384 400 000用科学记数法表示为（ ）
    A.3.844×108
    B.3.844×107
    C.3.844×109
    D.38.44×109

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市老板到批发中心选购甲、乙两种品牌的水杯。甲进货单价为3元、乙进货单价为4元；考虑各种因素，预计购进乙品牌水杯的数量y（个）与甲品牌水杯的数量x（个）之间的函数关系如图所示．

    （1）根据图象，求y与x之间的函数关系式；

    （2）若该超市每销售1个甲水杯可获利0.5元，每销售1个乙水杯可获利1元。请写出获利W（元）与x（个）的函数关系式；

    （3）在（2）的条件下，超市老板决定用不超过700元购进甲、乙两种品牌的水杯，且这两种品牌的水杯全部售出后获利不低于149元，问该超市有几种进货方案？哪种方案能使获利最大？最大获利为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，

    （1）求证：四边形ADCE为矩形；

    （2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．

    查看答案和解析>>

    同步练习册答案