
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

【答案】(1)证明见解析(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
【解析】试题分析:(1)根据矩形的有三个角是直角的四边形是矩形,已知CE⊥AN,AD⊥BC,所以求证∠DAE=90°,可以证明四边形ADCE为矩形.
(2)根据正方形的判定,我们可以假设当AD=![]() BC,由已知可得,DC=
BC,由已知可得,DC=![]() BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
试题解析:(1)证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=![]() ×180°=90°,
×180°=90°,
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
理由:∵AB=AC,
∴∠ACB=∠B=45°,
∵AD⊥BC,
∴∠CAD=∠ACD=45°,
∴DC=AD,
∵四边形ADCE为矩形,
∴矩形ADCE是正方形.
∴当∠BAC=90°时,四边形ADCE是一个正方形.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
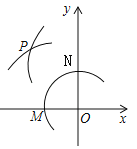
A. a=b B. 2a﹣b=1 C. 2a+b=﹣1 D. 2a+b=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22=8,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2010年5月27日,上海世博会参观人数达到37.7万人,这个数用科学记数法表示为( )
A.0.377×106人
B.3.77×105人
C.3.77×104人
D.377×103人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com