
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,8为半径的圆与
为圆心,8为半径的圆与![]() 轴交于
轴交于![]() ,
,![]() 两点,过
两点,过![]() 作直线
作直线![]() 与
与![]() 轴负方向相交成
轴负方向相交成![]() 的角,且交
的角,且交![]() 轴于
轴于![]() 点,以点
点,以点![]() 为圆心的圆与
为圆心的圆与![]() 轴相切于点
轴相切于点![]() .
.
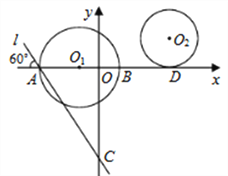
(1)求直线![]() 的解析式;
的解析式;
(2)将![]() 以每秒1个单位的速度沿
以每秒1个单位的速度沿![]() 轴向左平移,当
轴向左平移,当![]() 第一次与
第一次与![]() 外切时,求
外切时,求![]() 平移的时间.
平移的时间.
【答案】(1)直线![]() 的解析式为:
的解析式为:![]() .(2)
.(2)![]() 平移的时间为5秒.
平移的时间为5秒.
【解析】(1)求直线的解析式,可以先求出A、C两点的坐标,就可以根据待定系数法求出函数的解析式.
(2)设⊙O2平移t秒后到⊙O3处与⊙O1第一次外切于点P,⊙O3与x轴相切于D1点,连接O1O3,O3D1.
在直角△O1O3D1中,根据勾股定理,就可以求出O1D1,进而求出D1D的长,得到平移的时间.
(1)由题意得![]() ,
,
∴![]() 点坐标为
点坐标为![]() .
.
∵在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
由![]() 过
过![]() 、
、![]() 两点,
两点,
得![]() ,
,
解得![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() .
.
(2)如图,设![]() 平移
平移![]() 秒后到
秒后到![]() 处与
处与![]() 第一次外切于点
第一次外切于点![]() ,
,
![]() 与
与![]() 轴相切于
轴相切于![]() 点,连接
点,连接![]() ,
,![]() .
.
则![]() ,
,
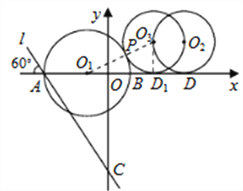
∵![]() 轴,∴
轴,∴![]() ,
,
在![]() 中,
中,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() (秒),
(秒),
∴![]() 平移的时间为5秒.
平移的时间为5秒.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.

(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图,根据给出的数轴,解答下面的问题:
![]()
(1)已知点![]() 表示的数分别为6,-4,观察数轴,与点
表示的数分别为6,-4,观察数轴,与点![]() 距离为5的点所表示的数是 ,
距离为5的点所表示的数是 ,![]() 两点之间的距离为 ;
两点之间的距离为 ;
(2)若点![]() 到点
到点![]() ,点
,点![]() 的距离相等,观察数轴并结合所学知识求点
的距离相等,观察数轴并结合所学知识求点![]() 表示的数;
表示的数;
(3)在(2)的条件下,若动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() 秒.则点
秒.则点![]() 表示的数是多少(用含字母
表示的数是多少(用含字母![]() 的式子表示);当
的式子表示);当![]() 等于多少秒时,
等于多少秒时,![]() 之间的距离为3个单位长度.
之间的距离为3个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列所给条件中,不能判断两个直角三角形全等的是( )
A. 一个锐角和这个锐角的对边对应相等B. 一个锐角与斜边对应相等
C. 两锐角对应相等D. 一锐角和一边对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、以两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树状图或列表的方法列出所有可能的结果;
(2)这样的游戏规则是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,BD平分∠ABC,CE平分∠ACB的邻补角∠ACM,若∠BDC=130°,∠E=50°,则∠BAC的度数是_______.
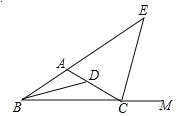
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com