
【题目】如图,在![]() 中,
中,![]() 、
、![]() 分别垂直平分
分别垂直平分![]() 和
和![]() ,交
,交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 与
与![]() 相交于点
相交于点![]()
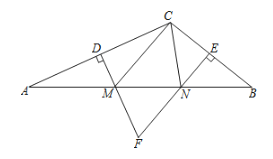
(1)若![]() 的周长为
的周长为![]() ,求
,求![]() 的长;
的长;
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)15cm;(2)20°.
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AM=CM,BN=CN,然后求出△CMN的周长=AB;
(2)根据三角形的内角和定理列式求出∠MNF+∠NMF,再求出∠A+∠B,根据等边对等角可得∠A=∠ACM,∠B=∠BCN,然后利用三角形的内角和定理列式计算即可得解.
解:(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB,
∵△CMN的周长为15cm,
∴AB=15cm;
(2)∵∠MFN=80°,
∴∠MNF+∠NMF=180°80°=100°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=100°,
∴∠A+∠B=90°∠AMD+90°∠BNE=180°100°=80°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°2(∠A+∠B)=180°2×80°=20°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,8为半径的圆与
为圆心,8为半径的圆与![]() 轴交于
轴交于![]() ,
,![]() 两点,过
两点,过![]() 作直线
作直线![]() 与
与![]() 轴负方向相交成
轴负方向相交成![]() 的角,且交
的角,且交![]() 轴于
轴于![]() 点,以点
点,以点![]() 为圆心的圆与
为圆心的圆与![]() 轴相切于点
轴相切于点![]() .
.
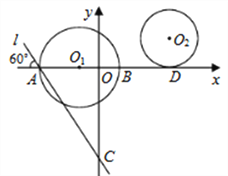
(1)求直线![]() 的解析式;
的解析式;
(2)将![]() 以每秒1个单位的速度沿
以每秒1个单位的速度沿![]() 轴向左平移,当
轴向左平移,当![]() 第一次与
第一次与![]() 外切时,求
外切时,求![]() 平移的时间.
平移的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
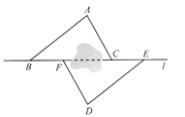
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一直径是![]() 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
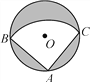
(1)AB的长为多少米?
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面半径为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
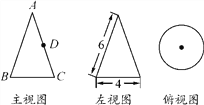
【题目】如图所示是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体上的点B出发,沿表面爬到AC的中点D,请你求出这条路线的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据阅读材料,回答问题.
材料:如图所示,有公共端点(O)的两条射线组成的图形叫做角(![]() ).如果一条射线(
).如果一条射线(![]() )把一个角(
)把一个角(![]() )分成两个相等的角(
)分成两个相等的角(![]() 和
和![]() ),这条射线(
),这条射线(![]() )叫做这个角的平分线.这时,
)叫做这个角的平分线.这时,![]() (或
(或![]() ).
).
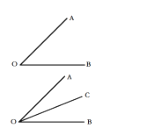
问题:平面内一定点A在直线![]() 的上方,点O为直线
的上方,点O为直线![]() 上一动点,作射线
上一动点,作射线![]() ,
,![]() ,
,![]() ,当点O在直线
,当点O在直线![]() 上运动时,始终保持
上运动时,始终保持![]() ,
,![]() ,将射线
,将射线![]() 绕点O顺时针旋转60°得到射线
绕点O顺时针旋转60°得到射线![]() .
.
(1)如图1,当点O运动到使点A在射线![]() 的左侧时,若
的左侧时,若![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
(2)当点O运动到使点A在射线![]() 的左侧,
的左侧,![]() 时,求
时,求![]() 的值;
的值;
(3)当点O运动到某一时刻时,![]() ,直接写出此时
,直接写出此时![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
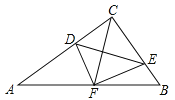
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中有一个黑球![]() 和两个白球
和两个白球![]() (除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(1)小丽第一次从袋子中摸出一个球不放回,第二次又从袋子中摸出一个球,则小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出一个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出一个球,则小强两次都摸到白球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com