
【题目】如图,有一直径是![]() 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
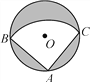
(1)AB的长为多少米?
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面半径为多少米?
科目:初中数学 来源: 题型:
【题目】下列所给条件中,不能判断两个直角三角形全等的是( )
A. 一个锐角和这个锐角的对边对应相等B. 一个锐角与斜边对应相等
C. 两锐角对应相等D. 一锐角和一边对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,BD平分∠ABC,CE平分∠ACB的邻补角∠ACM,若∠BDC=130°,∠E=50°,则∠BAC的度数是_______.
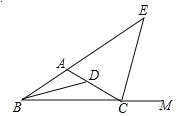
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买![]() 型和
型和![]() 型课桌凳共
型课桌凳共![]() 套,经招标,购买一套
套,经招标,购买一套![]() 型课桌凳比购买一套
型课桌凳比购买一套![]() 型课桌凳少用
型课桌凳少用![]() 元,且购买
元,且购买![]() 套
套![]() 型和
型和![]() 套
套![]() 型课桌凳共需
型课桌凳共需![]() 元.
元.
(1)求购买一套![]() 型课桌凳和一套
型课桌凳和一套![]() 型课桌凳各需多少元?
型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳的总费用不能超过![]() 元,并且购买
元,并且购买![]() 型课桌凳的数量不能超过
型课桌凳的数量不能超过![]() 型课桌凳数量的
型课桌凳数量的![]() ,求该校本次购买
,求该校本次购买![]() 型和
型和![]() 型课桌凳共有几种购买方案?怎样的方案使总费用最低?并求出最低消费.
型课桌凳共有几种购买方案?怎样的方案使总费用最低?并求出最低消费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
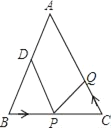
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)OA= cm,OB= cm.
(2)若点C是线段AO上一点,且满足AC=CO+CB,求CO的长.
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为t(s),当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP﹣OQ=8.
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后立即返回,又以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
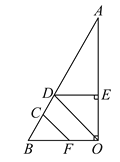
【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.
证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了拉动内需,全国各地汽车购置税补贴活动正式开始.重庆长安汽车经销商在出台前一个月共售出长安SUV汽车SC35的手动型和自动型共960台,政策出台后的第一月售出这两种型号的汽车共1228台,其中手动型和自动型汽车的销售量分别比政策出台前一个月增长30%和25%.
(1)在政策出台前一个月,销售的手动型和自动型汽车分别为多少台;
(2)若手动型汽车每台价格为9万元,自动型汽车每台价格为10万元.根据汽车补贴政策,政府按每台汽车价格的5%给购买汽车的用户补贴,问政策出台后的第一个月,政府对这1228台汽车用户共补贴了多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com