
【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.
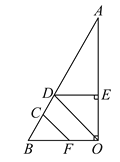
证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
【答案】①垂直定义②同位角相等,两直线平行③两直线平行,内错角相等 ④已知⑤等量代换 ⑥同位角相等,两直线平行
【解析】由DE与BO都与AO垂直,利用垂直定义得到一对直角相等,利用同位角相等两直线平行得到DE与BO平行,利用两直线平行得到一对内错角相等,再由已知的一对角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得到CF与DO平行.
解:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°(垂直的定义)
∴DE∥BO(同位角相等两直线平行)
∴∠EDO=∠DOF(两直线平行内错角相等)
又∵∠CFB=∠EDO(已知)
∴∠DOF=∠CFB(等量代换)
∴CF∥DO(同位角相等两直线平行).
故答案为:垂直的定义;同位角相等两直线平行;两直线平行内错角相等;已知;等量代换;同位角相等两直线平行


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】2016年5月下旬,中国大数据博览会在贵阳举行,参加此次大会的人数约有89000人,将89000用科学记数法表示为( )
A.89×103
B.8.9×103
C.8.9×104
D.0.89×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,时钟是我们常见的生活必需品,其中蕴含着许多数学知识.

(1)我们知道,分针和时针转动一周都是 度,分针转动一周是 分钟,时针转动一周有12小时,等于720分钟;所以,分针每分钟转动 度,时针每分钟转动 度.
(2)从5:00到5:30,分针与时针各转动了多少度?
(3)请你用方程知识解释:从1:00开始,在1:00到2:00之间,是否存在某个时刻,时针与分针在同一条直线上?若不存在,说明理由;若存在,求出从1:00开始经过多长时间,时针与分针在同一条直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中能用平方差公式计算的是( )
A.(a+3b)(3a﹣b)
B.(3a﹣b)(3a﹣b)
C.(3a﹣b)(﹣3a+b)
D.(3a﹣b)(3a+b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.
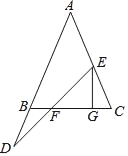
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com