
【题目】如图,时钟是我们常见的生活必需品,其中蕴含着许多数学知识.

(1)我们知道,分针和时针转动一周都是 度,分针转动一周是 分钟,时针转动一周有12小时,等于720分钟;所以,分针每分钟转动 度,时针每分钟转动 度.
(2)从5:00到5:30,分针与时针各转动了多少度?
(3)请你用方程知识解释:从1:00开始,在1:00到2:00之间,是否存在某个时刻,时针与分针在同一条直线上?若不存在,说明理由;若存在,求出从1:00开始经过多长时间,时针与分针在同一条直线上.
【答案】(1)360,60,6,0.5.(2)15°;(3)经过![]() 分钟或
分钟或![]() 分钟时针与分针在同一条直线上.
分钟时针与分针在同一条直线上.
【解析】试题分析:(1)利用钟表盘的特征解答.表盘一共被分成60个小格,每一个小格所对角的度数是6°;
(2)从5:00到5:30,分针转动了30个格,时针转动了2.5个格,即可求解;
(3)时针与分针在同一条直线上,分两种情况:①分针与时针重合;②分针与时针成180°,
设出未知数,,列出方程求解即可.
试题解析:(1)分针和时针转动一周都是360度,分针转动一周是60分钟,时针转动一周有12小时,等于720分钟;所以,分针每分钟转动360°÷60=6度,时针每分钟转动360°÷720=0.5度.
故答案为:360,60,6,0.5.
(2)从5:00到5:30,分针转动了:6°×30=180°,时针转动了6°×2.5=15°;
(3)从1:00开始,在1:00到2:00之间,存在某个时刻,时针与分针在同一条直线上.
设x分钟分针与时针重合,
则,0.5+30°=6x
解得 ![]()
设y分钟分针与时针成180°,
0.5y+30°+180°=6y
解得 ![]()
∴经过![]() 分钟或
分钟或![]() 分钟时针与分针在同一条直线上.
分钟时针与分针在同一条直线上.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AC=BC,分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE,AE与BD相交于点F,连接CF并延长交AB于点G.求证:CG垂直平分AB. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,王刚在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触,此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过计算说明.(参考数据: ![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=50°,∠DOE=35°,求∠BOD的度数;
(2)若∠AOE=160°,∠COD=40°,求∠AOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水果商贩在批发市场按1.8元/千克批发了若干千克的苹果进城出售,为了方便,他带了一些零钱备用,他先按市场价出售一些后,又每千克下降0.5元将剩余的苹果降价售完,这时他手中的钱(含备用零钱)是450元.售出苹果x千克与他手中持有的钱数y元(含备用零钱)的关系如图所示,则这个水果商贩一共赚_____元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.
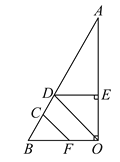
证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com