
【题目】如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=50°,∠DOE=35°,求∠BOD的度数;
(2)若∠AOE=160°,∠COD=40°,求∠AOB的度数.

【答案】(1)∠BOD==85°;∠AOB=40°.
【解析】试题分析:(1)、根据角平分线的性质分别求出∠COB和∠COD的度数,然后根据∠BOD=∠BOC+∠COD得出答案;(2)、根据OD是角平分线求出∠COE的度数,然后根据∠AOC=∠AOE-∠COE求出∠AOC的度数,最后根据OB为角平分线得出∠AOB的度数.
试题解析:解:(1)∵OB是∠AOC的平分线,OD是∠COE的平分线,∴∠COB=∠BOA=50°,∠COD=∠DOE=35°,∴∠BOD=∠COB+∠COD=50°+35°=85°.
(2)∵OD是∠COE的平分线,∴∠COE=2∠COD=2×40°=80°,∴∠AOC=∠AOE-∠COE=160°-80°=80°,
又∵OB是∠AOC的平分线,∴∠AOB=![]() ∠AOC=
∠AOC=![]() ×80°=40°.
×80°=40°.


科目:初中数学 来源: 题型:
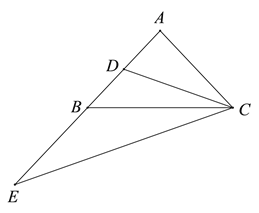
【题目】如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB至点E,使BE=AB,连接CE. 请你探究:
(1)当∠BAC为直角时,直接写出线段CE与CD之间的数量关系;
(2)当∠BAC为锐角或钝角时,(1)中的上述数量关系是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)依次为95、90、88,则小彤这学期的体育成绩为( )
A. 89 B. 90 C. 92 D. 93
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则下面结论错误的是( ) 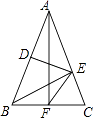
A.BF=EF
B.DE=EF
C.∠EFC=45°
D.∠BEF=∠CBE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,时钟是我们常见的生活必需品,其中蕴含着许多数学知识.

(1)我们知道,分针和时针转动一周都是 度,分针转动一周是 分钟,时针转动一周有12小时,等于720分钟;所以,分针每分钟转动 度,时针每分钟转动 度.
(2)从5:00到5:30,分针与时针各转动了多少度?
(3)请你用方程知识解释:从1:00开始,在1:00到2:00之间,是否存在某个时刻,时针与分针在同一条直线上?若不存在,说明理由;若存在,求出从1:00开始经过多长时间,时针与分针在同一条直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
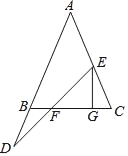
【题目】如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=3,BC=4.当平行四边形ABCD的面积最大时。下列结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com