【题目】如图，在△ABC中，AB=AC，CD是AB边上的中线，延长AB至点E，使BE=AB，连接CE. 请你探究：

（1）当∠BAC为直角时，直接写出线段CE与CD之间的数量关系；

（2）当∠BAC为锐角或钝角时，（1）中的上述数量关系是否仍然成立？若成立，请给出证明；若不成立，请说明理由。

参考答案：

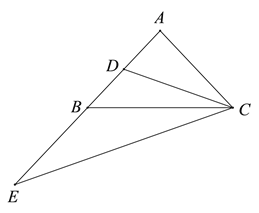
【答案】（1）CE=2CD；（2）仍然成立

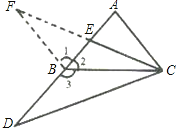
【解析】试题分析：（1）如图，延长CE到F，使EF=CE，连接FB．由CE是AB边上的中线，∠BEF=∠AEC，可证得△AEC≌△BEF，进而得∠1=∠A，FB=BD，从而可得△CDB≌△CFB，即可得到结果;

（2）根据上面的方法，直接可画图证明即可.

试题解析：（1）CE=2CD；

延长CE到F，使EF=CE，连接FB，

∵CE是AB边上的中线，

∴AE=BE，

又∵∠BEF=∠AEC，

∴△AEC≌△BEF，

∴FB=AC，∠1=∠A，

∵BD=AB，

∴FB=BD，

∵∠3=∠A+∠ACB=∠1+∠2，即∠CBD=∠CBF，

又∵BC为公共边，

∴△CDB≌△CFB，

∴CD=CF=2CE，

即2CE=CD

（2）仍然成立. 例如取AC中点M,连接BM. 证法较多，略。

关闭