
| A. | $\frac{3}{2}\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
分析 连接OB、OC,作OD⊥BC于D,则∠ODB=90°,BD=CD,∠OBC=30°,由含30°角的直角三角形的性质得出OD,由勾股定理求出BD,得出BC,△ABC的面积=3S△OBC,即可得出结果.
解答 解:如图所示: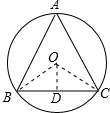
连接OB、OC,作OD⊥BC于D,
则∠ODB=90°,BD=CD,∠OBC=30°,
∴OD=$\frac{1}{2}$OB=1,
∴BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴BC=2BD=2$\sqrt{3}$,
∴△ABC的面积=3S△OBC=3×$\frac{1}{2}$×BC×OD=3×$\frac{1}{2}$×2$\sqrt{3}$×1=3$\sqrt{3}$.
故选:B.
点评 本题考查了等边三角形的性质、垂径定理、勾股定理、三角形面积的计算;熟练掌握正三角形和圆的关系,并能进行推理计算是解决问题的关键.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:选择题
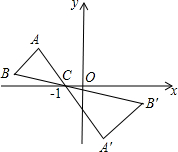 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是( )
如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是( )| A. | 3 | B. | -3 | C. | -4 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
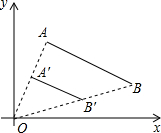 如图,线段AB的两个端点坐标分别为A(1,4),B(6,2),以原点O为位似中心,将线段AB缩小后得到线段A′B′.若AB=2A′B′,则端点B′的坐标为( )
如图,线段AB的两个端点坐标分别为A(1,4),B(6,2),以原点O为位似中心,将线段AB缩小后得到线段A′B′.若AB=2A′B′,则端点B′的坐标为( )| A. | (2,2) | B. | (3,2) | C. | (2,1) | D. | (3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
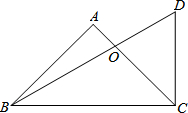 一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.
一次综合实践活动中,小明同学拿到一只含45°角的三角板和一只含30°角的三角板,如图放置恰好有一边重合,则S△ODC:S△OAB的值为$\frac{3+\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
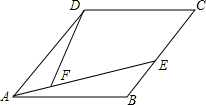 如图,四边形ABCD是菱形,点E在BC上,∠AFD=∠B,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一案的具体作法证明△ABG≌△DAF.
如图,四边形ABCD是菱形,点E在BC上,∠AFD=∠B,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一案的具体作法证明△ABG≌△DAF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
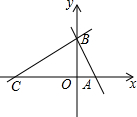 如图,平面直角坐标系中,直线y=-$\sqrt{3}x$+$\sqrt{3}$与坐标轴分别交于点A、B,且点C在x轴负半轴上,且AB:AC=1:2.
如图,平面直角坐标系中,直线y=-$\sqrt{3}x$+$\sqrt{3}$与坐标轴分别交于点A、B,且点C在x轴负半轴上,且AB:AC=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
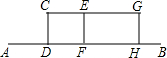 某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com