
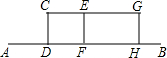
 某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).分析 (1)利用中心投影的定义画图;
(2)设小明原来的速度为xm/s,则CE=2xm,AM=AF-MF=(4x-1.2)m,EG=2×1.5x=3xm,BM=AB-AM=12-(4x-1.2)=13.2-4x,根据相似三角形的判定方法得到△OCE∽△OAM,△OEG∽△OMB,则$\frac{CE}{AM}$=$\frac{OE}{OM}$,$\frac{EG}{BM}$=$\frac{OE}{OM}$,所以$\frac{CE}{AM}$=$\frac{EG}{BM}$,即$\frac{2x}{4x-1.2}$=$\frac{3x}{13.2-4x}$,然后解方程解决.
解答 解:(1)如图,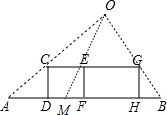
(2)设小明原来的速度为xm/s,则CE=2xm,AM=AF-MF=(4x-1.2)m,EG=2×1.5x=3xm,BM=AB-AM=12-(4x-1.2)=13.2-4x,
∵点C,E,G在一条直线上,CG∥AB,
∴△OCE∽△OAM,△OEG∽△OMB,
∴$\frac{CE}{AM}$=$\frac{OE}{OM}$,$\frac{EG}{BM}$=$\frac{OE}{OM}$,
∴$\frac{CE}{AM}$=$\frac{EG}{BM}$,即$\frac{2x}{4x-1.2}$=$\frac{3x}{13.2-4x}$,解得x=1.5,
经检验x=1.5为方程的解,
∴小明原来的速度为1.5m/s.
答:小明原来的速度为1.5m/s.
点评 本题考查了相似三角形的应用:从实际问题中抽象出几何图形,然后利用相似比计算相应线段的长.也考查了中心投影.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{2}\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 数据x | 70<x<79 | 80<x<89 | 90<x<99 |
| 个数 | 800 | 1300 | 900 |
| 平均数 | 78.1 | 85 | 91.9 |
| A. | 92.16 | B. | 85.23 | C. | 84.73 | D. | 77.97 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 119×106 | B. | 11.9×107 | C. | 1.19×108 | D. | 0.119×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{106960}{x+500}$-$\frac{50760}{x}$=20 | B. | $\frac{50760}{x}$-$\frac{106960}{x+500}$=20 | ||
| C. | $\frac{106960}{x+20}$-$\frac{50760}{x}$=500 | D. | $\frac{50760}{x}$-$\frac{106960}{x+20}$=500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com