
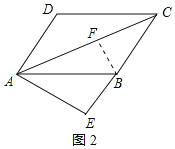
【题目】已知ABCD,过点A作BC的垂线,垂足为E,∠BAE=30°,BC=2,AE=![]() ,则点B到直线AC的距离为_____.
,则点B到直线AC的距离为_____.
【答案】![]() 或1
或1
【解析】
分两种情况, 进行讨论解答,第一种:作BF⊥AC于F,找到△ABC是等边三角形,再用勾股定理找到距离;第二种作BF⊥AC于F,BE=1,AB=2,∠ABE=60°,得到BF=![]() BC=1.
BC=1.
分两种情况:
①如图1所示:作BF⊥AC于F,
∵AE⊥BC,
∴∠AEB=90°,
∵∠BAE=30°,AE=![]() ,
,
∴BE=1,AB=2,∠ABE=60°,
∵BC=2=AB,
∴△ABC是等边三角形,
∴AC=BC=2,
∵BF⊥AC,
∴CF=![]() AC=1,
AC=1,
∴BF=![]() =
=![]() ;
;
②如图2所示:作BF⊥AC于F,
∵AE⊥BC,
∴∠AEB=90°,
∵∠BAE=30°,AE=![]() ,
,
∴BE=1,AB=2,∠ABE=60°,
∵BC=2=AB,
∴∠BCA=∠BAC=30°,
∴BF=![]() BC=1;
BC=1;
综上所述,点B到直线AC的距离为![]() 或1;
或1;
故答案为:![]() 或1.
或1.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
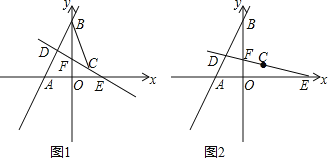
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB=![]() OA,直线l2:y=k2x+b经过点C(
OA,直线l2:y=k2x+b经过点C(![]() ,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
(1)求直线l1的解析式;
(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欧尚超市准备代销一款运动鞋,每双的成本是160元,为了合理定价,投放市场进行试销.据市场调查,销售单价是200元时,每天的销售量是40双,而销售单价每降低1元,每天就可多售出6双(售价不得低于160元/双),设每双降低售价x元(x为正整数),每天的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每双运动鞋的售价定为多少元时,每天可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
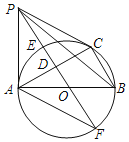
【题目】如图,⊙O是△ABC的外接圆,AB是直径,OD⊥AC,垂足为D点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PB,PC,且满足∠PCA=∠ABC
(1)求证:PA=PC;
(2)求证:PA是⊙O的切线;
(3)若BC=8,![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O,连接AC、BD,2∠BDC+∠ADB=180°.
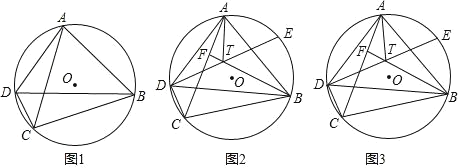
(1)如图1,求证:AC=BC;
(2)如图2,E为⊙O上一点,![]() =
=![]() ,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+
,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+![]() ∠ABD,求证:AT平分∠DAB;
∠ABD,求证:AT平分∠DAB;
(3)在(2)的条件下,DT=TE,AD=8,BD=12,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个单位为 1 的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在 x 轴上、斜边长分别为 2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2019的横坐标为( )
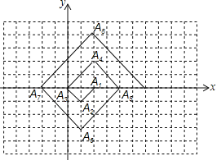
A.-1008B.2C.1D.1011
查看答案和解析>>
科目:初中数学 来源: 题型:
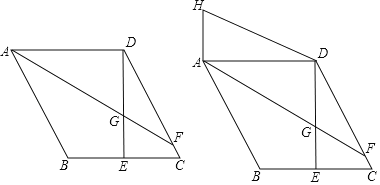
【题目】如图,在平行四边形ABCD中,过点D作DE⊥BC交BC于点E,且DE=AD,F为DC上一点,且AD=FD,连接AF与DE交于点G.
(1)若∠C=60°,AB=2,求GF的长;
(2)过点A作AH⊥AD,且AH=CE,求证:AB=DG+AH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com