
【题目】四边形ABCD内接于⊙O,连接AC、BD,2∠BDC+∠ADB=180°.
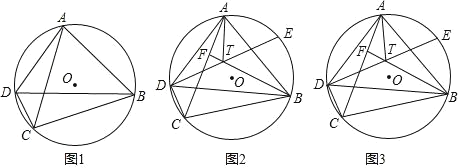
(1)如图1,求证:AC=BC;
(2)如图2,E为⊙O上一点,![]() =
=![]() ,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+
,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+![]() ∠ABD,求证:AT平分∠DAB;
∠ABD,求证:AT平分∠DAB;
(3)在(2)的条件下,DT=TE,AD=8,BD=12,求DE的长.
【答案】(1)见解析;(2)见解析;(3)8![]()
【解析】
(1)只要证明∠CAB=∠CBA即可.
(2)如图2中,作TH⊥AD于H,TR⊥BD于R,TL⊥AB于L.想办法证明TL=TH即可解决问题.
(3)如图3中,连接EA,EB,作EG⊥AB,TH⊥AD于H,TR⊥BD于R,TL⊥AB于L,AQ⊥BD于Q.证明△EAG≌△TDH(AAS),推出AG=DH,证明Rt△TDR≌Rt△TDH(HL),推出DH=DR,同理可得AL=AH,BR=BL,设DH=x,则AB=2x,
由S△ADB=![]() BDAQ=
BDAQ=![]() ADh+
ADh+![]() ABh+
ABh+![]() DBh,可得AQ=
DBh,可得AQ=![]() h,再根据sin∠BDE=sin∠ADE,sin∠AED=sin∠ABD,构建方程组求出m即可解决问题.
h,再根据sin∠BDE=sin∠ADE,sin∠AED=sin∠ABD,构建方程组求出m即可解决问题.
解:(1)如图1中,
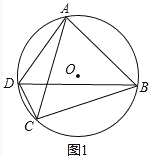
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
即∠ADB+∠BDC+∠ABC=180°,
∵2∠BDC+∠ADB=180°,
∴∠ABC=∠BDC,
∵∠BAC=∠BDC,
∴∠BAC=∠ABC,
∴AC=BC.
(2)如图2中,作TH⊥AD于H,TR⊥BD于R,TL⊥AB于L.
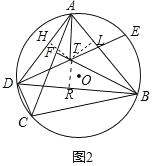
∵∠BFC=∠BAC+∠ABF,∠BAC=∠BDC,
∴∠BFC=∠BDC+∠ABF,
∵∠BFC=∠BDC+![]() ∠ABD,
∠ABD,
∴∠ABF=![]() ∠ABD,
∠ABD,
∴BT平分∠ABD,
∵![]() =
=![]()
∴∠ADE=∠BDE,
∴DT平分∠ADB,
∵TH⊥AD于H,TR⊥BD于R,TL⊥AB于L.
∴TR=TL,TR=TH,
∴TL=TH,
∴AT平分∠DAB.
(3)如3中,连接EA,EB,作EG⊥AB,TH⊥AD于H,TR⊥BD于R,TL⊥AB于L,AQ⊥BD于Q.
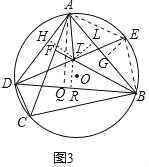
∵![]() =
=![]()
∴∠EAB=∠EDB=∠EDA,AE=BE,
∵∠TAE=∠EAB+∠TAB,∠ATE=∠EDA+∠DAT,
∴∠TAE=∠ATE,
∴AE=TE,
∵DT=TE,
∴AE=DT,
∵∠AGE=∠DHT=90°,
∴△EAG≌△TDH(AAS),
∴AG=DH,
∵AE=EB,EG⊥AB,
∴AG=BG,
∴2DH=AB,
∵Rt△TDR≌Rt△TDH(HL),
∴DH=DR,同理可得AL=AH,BR=BL,
设DH=x,则AB=2x,
∵AD=8,DB=12,
∴AL=AH=8﹣x,BR=12﹣x,AB=2x=8﹣x+12﹣x,
∴x=5,
∴DH=5,AB=10,
设TR=TL=TH=h,DT=m,
∵S△ADB=![]() BDAQ=
BDAQ=![]() ADh+
ADh+![]() ABh+
ABh+![]() DBh,
DBh,
∴12AQ=(8+12+10)h,
∴AQ=![]() h,
h,
∵sin∠BDE=sin∠ADE,可得![]() =
=![]() =
=![]() ,
,
sin∠AED=sin∠ABD,可得![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
= ,
,
解得m=4![]() 或﹣4
或﹣4![]() (舍弃),
(舍弃),
∴DE=2m=8![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲、乙人5场10次投篮命中次数如图
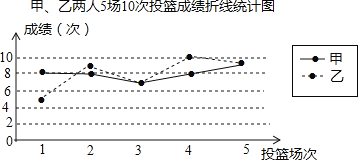
(1)填写表格.
平均数 | 众数 | 中位数 | 方差 | |
甲 | ______ | 8 | 8 | ______ |
乙 | 8 | ______ | ______ | 3.2 |
(2)①教练根据这5个成绩,选择甲参加投篮比赛,理由是什么?
②如果乙再投篮1场,命中8次,那么乙的投监成绩的方差将会怎样变化?(“变大”“变小”或”不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,且OA,OB分别与反比例函数y=![]() (x>0)、y=﹣
(x>0)、y=﹣![]() (x<0)的图象交于A,B两点,则sin∠OAB的值是( )
(x<0)的图象交于A,B两点,则sin∠OAB的值是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
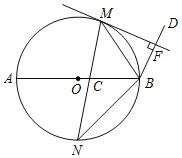
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=-![]() 与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
与一次函数y=kx+b的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;
(2)△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,
,![]() 是边
是边![]() 上一点,
上一点,![]() ,将
,将![]() ,
,![]() 分别沿折痕
分别沿折痕![]() ,
,![]() 向内折叠,点
向内折叠,点![]() ,
,![]() 在点
在点![]() 处重合,过点
处重合,过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() .则下列结论正确的有( )
.则下列结论正确的有( )
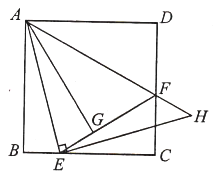
①![]() ;②
;②![]() 为等腰直角三角形;③点
为等腰直角三角形;③点![]() 是
是![]() 的中点;④
的中点;④![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在很多家庭都使用折叠型西餐桌来节省空间,两边翻开后成圆形桌面(如图1).餐桌两边AB和CD平行且相等(如图2),小华用皮带尺量出AC=2米,AB=1米,那么桌面翻成圆桌后,桌子面积会增加_____平方米.(结果保留π)
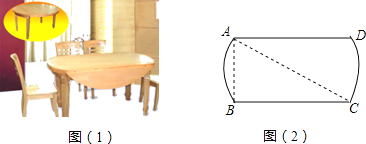
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.
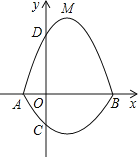
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com