
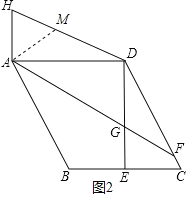
【题目】如图,在平行四边形ABCD中,过点D作DE⊥BC交BC于点E,且DE=AD,F为DC上一点,且AD=FD,连接AF与DE交于点G.
(1)若∠C=60°,AB=2,求GF的长;
(2)过点A作AH⊥AD,且AH=CE,求证:AB=DG+AH.
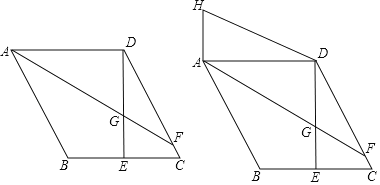
【答案】(1)GF=1;(2)证明见解析.
【解析】
(1)过G作GH⊥CD于H,根据三角形的内角和得到∠CDE=60°,根据平行四边形的性质得到AD∥BC,AB=CD=2,得到∠ADC=120°,解直角三角形即可得到结论;
(2)根据全等三角形的性质得到∠ADH=∠EDC,∠H=∠C,DH=DC,根据平行四边形的性质得到AB=CD,AB∥CD,推出∠DFA=![]() ∠C,在DH上截取HM=AH,得到∠HAM=∠HMA,求得∠DAM=
∠C,在DH上截取HM=AH,得到∠HAM=∠HMA,求得∠DAM=![]() ∠H,根据全等三角形的性质即可得到结论.
∠H,根据全等三角形的性质即可得到结论.
解:(1)如图1,过G作GH⊥CD于H,
∵DE⊥BC,
∴∠DEC=90°,
∵∠C=60°,
∴∠CDE=30°,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=2,
∴∠ADC=120°,
∵AD=DF,
∴∠DAF=∠DFA=30°,
∴∠GDF=∠DFG,
∴DG=GF,
∵CD=2,
∴DE=![]() CD=
CD=![]() ,
,
∴DF=![]() ,
,
∴HF=![]() DF=
DF=![]() ,
,
∴GF=1;
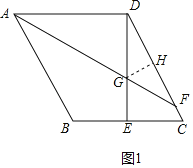
(2)∵AH⊥AD,DE⊥BC,
∴∠DAH=∠DEC=90°,
在△DAH与△DEC中,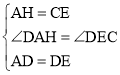 ,
,
∴△DAH≌△DEC(SAS),
∴∠ADH=∠EDC,∠H=∠C,DH=DC,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠DAB=∠C,∠DFA=∠BAF,
∵AD=DF,
∴∠DAF=∠DFA,
∴∠DFA=![]() ∠C,
∠C,
如图2,在DH上截取HM=AH,
∴∠HAM=∠HMA,
∴∠H=180°﹣2∠HAM,
∵∠MAD=90°﹣∠HAM,
∴∠DAM=![]() ∠H,
∠H,
∴∠MAD=∠GFD,
在△ADM与△FDG中,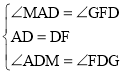 ,
,
∴△ADM≌△FDG(ASA),
∴DM=DG,
∵AB=CD=DH=HM+DM,
∴AB=AH+DG.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
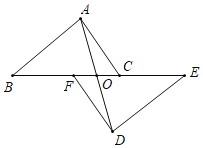
【题目】如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.
(1)求证:△ABC≌△DEF;
(2)求证:AD与BE互相平分;
(3)若BF=5,FC=4,直接写出EO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
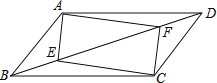
【题目】如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.
(1)求证:四边形AECF是平行四边形.
(2)若AF=EF,∠BAF=108°,∠CDF=36°,直接写出图中所有与AE相等的线段(除AE外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国的经济总量已居世界第二,人民富裕了,有的家庭拥有多种车型.小红家有A、B、C三种车型,已知3辆A型车的载重量与4辆B型车的载重量之和刚好等于2辆C型车的载重量;4辆B型车的载重量与1辆C型车的载重量之和刚好等于6辆A型车的载重量.现有一批货物,原计划用C型车10次可全部运完,由于C型车另有运输任务,现在安排A型车单独装运12次,余下的货物由B型车单独装运刚好可以全部运完,则B型车需单独装运_____次(每辆车每次都满载重量)
查看答案和解析>>
科目:初中数学 来源: 题型:
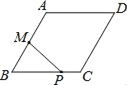
【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
A. 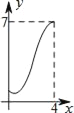 B.
B. 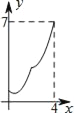 C.
C. 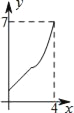 D.
D. 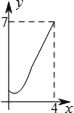
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条笔直的公路![]() 穿过草原,公路边有一卫生站
穿过草原,公路边有一卫生站![]() 距公路
距公路![]() 的地方有一居民点
的地方有一居民点![]() ,
,![]() 、
、![]() 之间的距离为
之间的距离为![]() .一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是
.一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是![]() ,在草地上行驶的最快速度是
,在草地上行驶的最快速度是![]() .问司机应在公路上行驶多少千米?全部所用的行车时间最短?最短时间为多少?
.问司机应在公路上行驶多少千米?全部所用的行车时间最短?最短时间为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图②所示,则图②中的b等于( )

A. ![]() B.
B. ![]() C. 5D. 4
C. 5D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com