
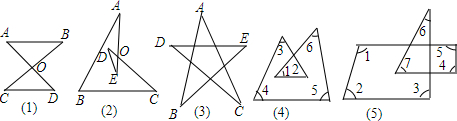
分析 本题利用“对顶三角形”的性质,逐一分析解答.
①∠1,∠2的和与∠D,∠E的和相等;
②∠1,∠2的和与∠D,∠E的和相等;
③∠1,∠2的和与∠7,∠8的和相等;
④∠6,∠7的和与∠8,∠9的和相等.
由多边形的内角和得出答案即可.
解答 解:如图:①∵∠1,∠2的和与∠D,∠E的和相等,
∴∠A+∠B+∠C+∠D+∠E=∠A+∠B+∠C+∠1+∠2=180°;
②∵∠1,∠2的和与∠D,∠E的和相等,
∴∠A+∠B+∠C+∠D+∠E=∠A+∠B+∠C+∠1+∠2=180°;
③∵∠1,∠2的和与∠7,∠8的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6=∠7+∠8+∠3+∠4+∠5+∠6=360°;
④∵∠6,∠7的和与∠8,∠9的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=540°.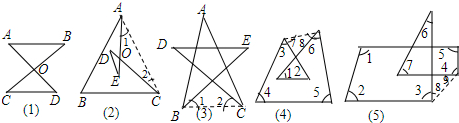
点评 本题考查了多边形的内角和,以及对顶角的性质,并利用题中新定义的“对顶三角形”的性质对题目进行分析解答,解题的关键在于找出个图形中的“对顶三角形”.


科目:初中数学 来源: 题型:选择题
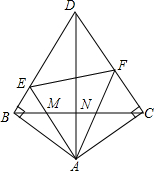 已知,如图所示四边形ABDC,DB⊥AB,CD⊥AC,AB=AC,∠EAF=∠BDC=60°,AE,AF分别交BC于点M,N,下列结论:
已知,如图所示四边形ABDC,DB⊥AB,CD⊥AC,AB=AC,∠EAF=∠BDC=60°,AE,AF分别交BC于点M,N,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
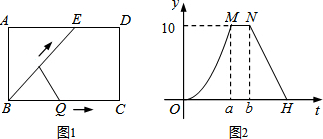
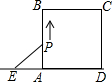 如图,延长正方形ABCD的边至点E,动点P从点A出发,沿拆线A-B-C-D匀速运动,则△PAE的面积S与运动时间t之间的大致图象是( )
如图,延长正方形ABCD的边至点E,动点P从点A出发,沿拆线A-B-C-D匀速运动,则△PAE的面积S与运动时间t之间的大致图象是( )| A. | 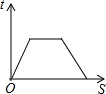 | B. | 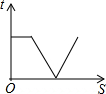 | C. | 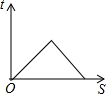 | D. | 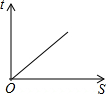 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
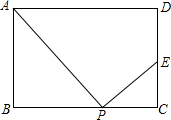 在矩形ABCD中,AB=4,AD=7,P是边BC上的任意一点(P与B、C不重合),作PE⊥AP,交CD边所在于点E.
在矩形ABCD中,AB=4,AD=7,P是边BC上的任意一点(P与B、C不重合),作PE⊥AP,交CD边所在于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com