
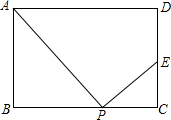
 在矩形ABCD中,AB=4,AD=7,P是边BC上的任意一点(P与B、C不重合),作PE⊥AP,交CD边所在于点E.
在矩形ABCD中,AB=4,AD=7,P是边BC上的任意一点(P与B、C不重合),作PE⊥AP,交CD边所在于点E.分析 (1)由矩形的性质得到∠ABP=∠PCE=90°,根据余角的性质得到∠BAP=∠EPC,于是得到结论;
(2)设BP=x,根据相似三角形的性质得到比例式,代入数据求得EC=$\frac{BP•PC}{AB}$=$\frac{x(7-x)}{4}$=-$\frac{1}{4}$(x-$\frac{7}{2}$)2+$\frac{49}{16}$,然后根据二次函数的最大值即可做出判断;
(3)过点P作PH⊥AD于H,设BP=x,则PC=PF=7-x,CE=EF=$\frac{x(7-x)}{4}$,DE=4-$\frac{x(7-x)}{4}$,PH=4,根据相似三角形的性质得到$\frac{DF}{EF}=\frac{PH}{PF}$,代入数据求得DF=x,HF=7-2x,然后根据勾股定理即可得到结论.
解答 解:(1)△ABP∽△PCE,
理由:∵∠ABP=∠PCE=90°,
∴∠BAP+∠APB=90°,
∵∠APE=90°,
∴∠APB+∠EPC=90°,
∴∠BAP=∠EPC,
∴△ABP∽△PCE;
(2)点E总在线段CD上,
理由:设BP=x,
∵△ABP∽△PCE,
∴EC=$\frac{BP•PC}{AB}$=$\frac{x(7-x)}{4}$=-$\frac{1}{4}$(x-$\frac{7}{2}$)2+$\frac{49}{16}$,
∴当x=$\frac{7}{2}$时,EC取得最大值$\frac{49}{16}$,
∵$\frac{49}{16}<$4,
∴点E总在线段CD上;
(3)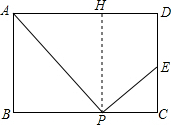 过点P作PH⊥AD于H,
过点P作PH⊥AD于H,
设BP=x,则PC=PF=7-x,CE=EF=$\frac{x(7-x)}{4}$,DE=4-$\frac{x(7-x)}{4}$,PH=4,
∵△PHF∽△FDE,
∴$\frac{DF}{EF}=\frac{PH}{PF}$,
即$\frac{DF}{\frac{x(7-x)}{4}}$=$\frac{4}{7-x}$,
∴DF=x,HF=7-2x,
在Rt△PHF中,PH2+HF2=PF2,
即42+(7-2x)2=(7-x)2,
解得:x1=2,x2=$\frac{8}{3}$,
∴tan∠APB=$\frac{AB}{BP}$=2或tan∠APB=$\frac{AB}{BP}$=$\frac{8}{3}$.
点评 本题考查了相似三角形的判定和性质,矩形的性质,勾股定理,二次函数的最大值,熟练掌握相似三角形的判定和性质是解题的关键.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:解答题
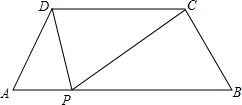 如图,梯形ABCD中,AB∥CD,AD=BC,∠A=60°,AD=4,CD=6,动点P从点A出发,沿AB方向以2单位长度/秒的速度向终点B运动,连接PC,PD,设点P运动的时间为t秒.
如图,梯形ABCD中,AB∥CD,AD=BC,∠A=60°,AD=4,CD=6,动点P从点A出发,沿AB方向以2单位长度/秒的速度向终点B运动,连接PC,PD,设点P运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
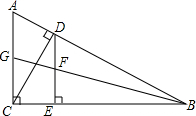 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,过点D作DE⊥BC,△BDE边DE上的中线BF延长线交AC于点G.
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,过点D作DE⊥BC,△BDE边DE上的中线BF延长线交AC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 中国数字音乐销售额/亿元 | 15.2 | 16.5 | 17.9 | 19.5 | 21.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
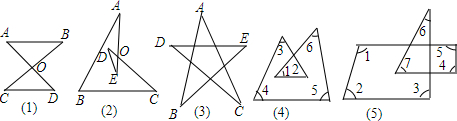
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
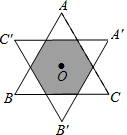 如图,已知等边三角形的面积为1,O为△ABC的中心(O到△ABC的各边距离相等),将△ABC绕中心O旋转60°,得到△A′B′C′,则△ABC与△A′B′C′重叠部分的面积为$\frac{2}{3}$.
如图,已知等边三角形的面积为1,O为△ABC的中心(O到△ABC的各边距离相等),将△ABC绕中心O旋转60°,得到△A′B′C′,则△ABC与△A′B′C′重叠部分的面积为$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在第10天、30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com