
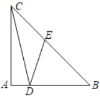
【题目】如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,那么
,那么![]() ________.
________.
【答案】![]()
【解析】
过点D作DF⊥BC于F,根据勾股定理即可求出BC,设![]() =x,根据等边对等角、三角形外角的性质和三角形的内角和定理即可求出∠DEB,再利用锐角三角函数即可求出EF和BF,最后根据BF+EF+CE=BC列出方程即可求出结论.
=x,根据等边对等角、三角形外角的性质和三角形的内角和定理即可求出∠DEB,再利用锐角三角函数即可求出EF和BF,最后根据BF+EF+CE=BC列出方程即可求出结论.
解:过点D作DF⊥BC于F

∵![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]()
∴AB=AC=1,∠B=45°
∴BC=![]() ,△BDF为等腰直角三角形,DF=BF
,△BDF为等腰直角三角形,DF=BF
设![]() =x
=x
∴∠ECD=∠EDC
∴∠DEB=∠ECD+∠EDC=2∠EDC
∴![]() =
=![]() (180°-∠EDC)=90°-
(180°-∠EDC)=90°-![]() ∠EDC
∠EDC
∵∠DEB+∠EDB+∠B=180°
∴2∠EDC+90°-![]() ∠EDC+45°=180°
∠EDC+45°=180°
解得:∠EDC=30°
∴∠DEB=60°
∴EF=DE·cos∠DEF=![]() x,DF=DE·sin∠DEF=
x,DF=DE·sin∠DEF=![]() x
x
∴BF=DF=![]() x
x
∵BF+EF+CE=BC
∴![]() x+
x+![]() x+x=
x+x=![]()
解得:x=![]()
即CE=![]()
故答案为:![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某公司计划投资![]() 万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为
万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为![]() 件,每件总成本为
件,每件总成本为![]() 万元,每件出厂价
万元,每件出厂价![]() 万元;流水生产线投产后,从第
万元;流水生产线投产后,从第![]() 年到第
年到第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)如下表:
(万元)如下表:
第 |
|
|
|
|
|
| ··· |
维修、保养费用累计 |
|
|
|
|
|
| ··· |
若上表中第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)与
(万元)与![]() 的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)投产第几年该公司可收回![]() 万元的投资?
万元的投资?
(3)投产多少年后,该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣m)2+2m(m≠0)经过原点,其顶点为P,与x轴的另一交点为A.
(1)P点坐标为 ,A点坐标为 ;(用含m的代数式表示)
(2)求出a,m之间的关系式;
(3)当m>0时,若抛物线y=a(x﹣m)2+2m向下平移m个单位长度后经过点(1,1),求此抛物线的表达式;
(4)若抛物线y=a(x﹣m)2+2m向下平移|m|个单位长度后与x轴所截的线段长,与平移前相比有什么变化?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:① 4ac<b2;② 方程ax2+bx+c=0的两个根分别是x1=-1,x2=3;③ 3a+c>0;④当 y>0时,x的取值范围是-1<x<3;⑤ 当x<0时,y随x的增大而增大.其中正确的结论序号有_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学以致用:问题1:怎样用长为![]() 的铁丝围成一个面积最大的矩形?
的铁丝围成一个面积最大的矩形?
小学时我们就知道结论:围成正方形时面积最大,即围成边长为![]() 的正方形时面积最大为
的正方形时面积最大为![]() .请用你所学的二次函数的知识解释原因.
.请用你所学的二次函数的知识解释原因.
思考验证:问题2:怎样用铁丝围一个面积为![]() 且周长最小的矩形?
且周长最小的矩形?
小明猜测:围成正方形时周长最小.
为了说明其中的道理,小明翻阅书籍,找到下面的结论:
在![]() 、
、![]() 均为正实数)中,若
均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() ,只有当
,只有当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
思考验证:证明:![]() 、
、![]() 均为正实数)
均为正实数)
请完成小明的证明过程:
证明:对于任意正实数![]() 、
、![]()
![]()
![]()
![]()
解决问题:
(1)若![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时取“
时取“![]() ”
” ![]() ;
;
(2)运用上述结论证明小明对问题2的猜测;
(3)填空:当![]() 时,
时,![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.

(1)点![]() 的坐标为___________;
的坐标为___________;
(2)连结![]() ,求
,求![]() 的正切值;
的正切值;
(3)抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() (
(![]() 、
、![]() 不重合),使
不重合),使![]() 与
与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
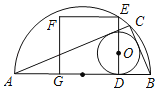
【题目】如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆上.
(1)当正方形的顶点F也在半圆弧上时,半圆的半径与正方形边长的比为 ;
(2)当正方形DEFG的面积为100,且△ABC的内切圆⊙O的半径r=4,求半圆的直径AB的值;
(3)若半圆的半径为R,直接写出⊙O半径r可取得的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
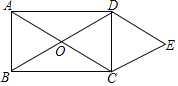
【题目】如图,矩形ABCD对角线AC、BD交于点O,边AB=6,AD=8,四边形OCED为菱形,若将菱形OCED绕点O旋转一周,旋转过程中OE与矩形ABCD的边的交点始终为M,则线段ME的长度可取的整数值为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
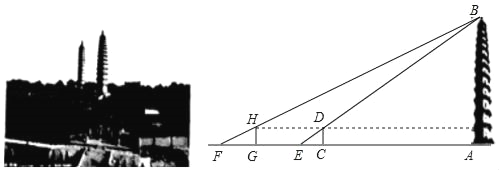
【题目】太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点C处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com