
【题目】已知抛物线y=a(x﹣m)2+2m(m≠0)经过原点,其顶点为P,与x轴的另一交点为A.
(1)P点坐标为 ,A点坐标为 ;(用含m的代数式表示)
(2)求出a,m之间的关系式;
(3)当m>0时,若抛物线y=a(x﹣m)2+2m向下平移m个单位长度后经过点(1,1),求此抛物线的表达式;
(4)若抛物线y=a(x﹣m)2+2m向下平移|m|个单位长度后与x轴所截的线段长,与平移前相比有什么变化?请直接写出结果.
【答案】(1)(m,2m),(2m,0);(2)a=﹣![]() ;(3)y=﹣(x﹣2)2+4或y=﹣2(x﹣1)2+2;(4)与x轴所截的线段长,与平移前相比是原来的
;(3)y=﹣(x﹣2)2+4或y=﹣2(x﹣1)2+2;(4)与x轴所截的线段长,与平移前相比是原来的![]() 或
或![]() 倍.
倍.
【解析】
(1)根据抛物线的顶点式即可求得P的坐标,得出对称轴为x=m,然后根据抛物线的对称性求得A的坐标;
(2)将x=0,y=0代入y=a(x﹣m)2+2m,化简即可求得a,m之间的关系式;
(3)先表示出当m>0时,抛物线y=a(x﹣m)2+2m向下平移m个单位长度后的解析式,再将点(1,1)代入,结合(2)中a和m的关系式,解得a和m的值,即可得出此抛物线的表达式;
(4)分两种情况:①a=﹣![]() ,m>0,a<0,②m<0,a>0,a=﹣
,m>0,a<0,②m<0,a>0,a=﹣![]() ,分别得出平移后的抛物线与坐标轴的交点,然后用含m的式子表示出与x轴所截的线段长,两者相比即可求得答案.
,分别得出平移后的抛物线与坐标轴的交点,然后用含m的式子表示出与x轴所截的线段长,两者相比即可求得答案.
解:(1)∵抛物线y=a(x﹣m)2+2m(m≠0),
∴P(m,2m),
∴对称轴为直线x=m,
∵抛物线y=a(x﹣m)2+2m(m≠0)经过原点,
∴A(2m,0).
故答案为:(m,2m),(2m,0).
(2)将x=0,y=0代入y=a(x﹣m)2+2m,得am2+2m=0,m≠0,
∴am+2=0.
∴am=﹣2,
∴a=﹣![]() .
.
(3)当m>0时,抛物线y=a(x﹣m)2+2m向下平移m个单位长度后,得y=a(x﹣m)2+m.
∵抛物线经过点(1,1),
∴a(1﹣m)2+m=1,
∴am2﹣2am+a+m=1.
又∵am=﹣2,
∴a=m﹣3.
把a=m﹣3代入am=﹣2,
解得a1=﹣1,m1=2或a2=﹣2,m2=1.
∴此抛物线的表达式为y=﹣(x﹣2)2+4或y=﹣2(x﹣1)2+2.
(4)①∵a=﹣![]()
∴当m>0时,a<0,
∵抛物线y=a(x﹣m)2+2m(m≠0)经过原点
∴y=ax2﹣2amx
向下平移m个单位后为y=ax2﹣2amx﹣m
平移前d=2m
平移后:令ax2﹣2amx﹣m=0得:
a(x﹣m)2=am2+m
化简得:(x﹣m)2=![]()
∴x1=m﹣![]() ,x2=m+
,x2=m+![]() m
m
∴d'=![]() m
m
∴![]() =
=![]() ;
;
②当m<0时,a>0,a=﹣![]()
原抛物线为y=ax2﹣2amx,向下平移|m|个单位后为y=ax2﹣2amx+m
平移前d=﹣2m
平移后:令ax2﹣2amx+m=0得:
a(x﹣m)2=am2+m
化简得:(x﹣m)2=![]() m2
m2
解得:x1=m﹣![]() m,x2=m+
m,x2=m+![]() m
m
∴d'=﹣![]() m
m
∴![]() =
=![]()
综上所述,与x轴所截的线段长,与平移前相比是原来的![]() 或
或![]() 倍.
倍.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
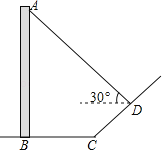
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+2经过点A(m,-2),将点A向右平移7个单位长度,得到点B,抛物线![]() 的顶点为C.
的顶点为C.
(1)求m的值和点B的坐标;
(2)求点C的坐标(用含n的代数式表示);
(3)若抛物线与线段AB只有一个公共点,结合函数图象,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
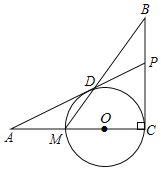
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是⊙O的切线;
(3)若AD=12,AM=MC,求PB和DM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有若干个仅颜色不同的红球和黑球,现往一个不透明的袋子里装进2个红球和3个黑球.
(1)随机摸出一个球是黑球的概率为 ;若先从袋子里取出m个红球(不放回),再从袋子里随机摸出一个球,将“摸到黑球”记为事件A.若事件A为必然事件,则m= ;
(2)若先从袋子里摸出一个球,放回后再摸出一个球,用列表法或画树状图法求出两次摸出的球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】装商店销售![]() 台
台![]() 型和
型和![]() 台
台![]() 型电脑的利润为
型电脑的利润为![]() 元,销售
元,销售![]() 台
台![]() 型和
型和![]() 台,
台, ![]() 型电脑的利润为
型电脑的利润为![]() 元.
元.
(1)求每台![]() 型电脑和
型电脑和![]() 型电脑的销售利润;
型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共 ![]() 台,其中
台,其中![]() 型电脑的进货量不超过
型电脑的进货量不超过![]() 型电脑的
型电脑的![]() 倍,购进
倍,购进![]() 型电脑
型电脑![]() 台,这
台,这![]() 台电脑的销售总利润为
台电脑的销售总利润为![]() 元.间该商店购进
元.间该商店购进![]() 型
型![]() 服各多少台.才能使销售利润
服各多少台.才能使销售利润![]() 最大?
最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年五月,我国南方某省A、B两市遭受严重洪涝灾害,邻近县市C、D决定调运物资支援A、B两市灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市,A市需要的物资比B市需要的物资少100吨.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)A、B两市各需救灾物资多少吨?
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
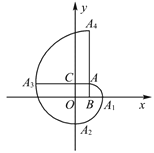
【题目】如图,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 的坐标为
的坐标为![]() ,弧
,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,继续以点
为半径的圆弧,继续以点![]() 为圆心,按上述作法得到的曲线
为圆心,按上述作法得到的曲线![]() …,称为正方形的“渐开线”,则点
…,称为正方形的“渐开线”,则点![]() 的坐标是______.
的坐标是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com