[题目]装商店销售台型和台型电脑的利润为元.销售台型和台. 型电脑的利润为元．(1)求每台型电脑和型电脑的销售利润,(2)该商店计划一次购进两种型号的电脑共台.其中型电脑的进货量不超过型电脑的倍.购进型电脑台.这台电脑的销售总利润为元．间该商店购进型服各多少台．才能使销售利润最大? 题目和参考答案——青夏教育精英家教网—

【题目】装商店销售台型和台型电脑的利润为元，销售台型和台，型电脑的利润为元．

（1）求每台型电脑和型电脑的销售利润；

（2）该商店计划一次购进两种型号的电脑共台，其中型电脑的进货量不超过型电脑的倍，购进型电脑台，这台电脑的销售总利润为元．间该商店购进型服各多少台．才能使销售利润最大?

【答案】（1）每台型电脑的销售利润为元，每台型电脑的销售利润为元；（2）商店购进型电脑台，型电脑台，才能使销售总利润最大．

【解析】

（1）设每台A型电脑销售利润为a元，每台B型电脑的销售利润为b元；然后根据销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元列出方程组，然后求解即可；
（2）根据总利润等于两种电脑的利润之和列式整理，再根据B型电脑的进货量不超过A型电脑的2倍列不等式求出x的取值范围，然后根据一次函数的增减性求出利润的最大值即可．

解：设每台型电脑的销售利润为元，每台型电脑的销售利润为元

则有

解得

答：每台型电脑的销售利润为元，每台型电脑的销售利润为元

根据题意得

即

解得

随的增大而减小．

为正整数

当最小时，

取最大值，

此时

答：商店购进型电脑台，型电脑台，才能使销售总利润最大．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】已知二次函数（是常数，）图象的对称轴是直线，其图象的一部分如图所示，下列说法中①；②；③当时，；④；⑤．正确的结论有（）

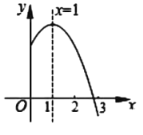
A.①②④B.②③④C.①③⑤D.①②③④⑤

查看答案和解析>>

科目：初中数学 来源： 题型：

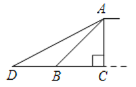
【题目】某市为了缓解城市交通压力，决定修建人行天桥，原设计天桥的楼梯与地面的夹角为45°（∠ABC=45°），BC=4.2 m，后考虑安全因素，将楼梯角B移到CB的延长线上点D处，使∠ADC=23°（如图所示）．求BD的长(精确到0.1 m)．（参考数据：sin 67°≈0.92，cos 67°≈0.39，tan 67°≈2.36）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在边长为1的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点O，则tan∠AOD=________.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知抛物线y＝a（x﹣m）2+2m（m≠0）经过原点，其顶点为P，与x轴的另一交点为A．

（1）P点坐标为　　，A点坐标为　　；（用含m的代数式表示）

（2）求出a，m之间的关系式；

（3）当m＞0时，若抛物线y＝a（x﹣m）2+2m向下平移m个单位长度后经过点（1，1），求此抛物线的表达式；

（4）若抛物线y＝a（x﹣m）2+2m向下平移|m|个单位长度后与x轴所截的线段长，与平移前相比有什么变化？请直接写出结果．

查看答案和解析>>

科目：初中数学 来源： 题型：

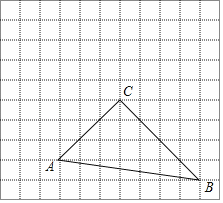
【题目】如图，在每个小正方形的边长为1的网格中，△ABC的顶点A、B、C均在格点上．

（1）∠ACB的大小为　　；

（2）在如图所示的网格中以A为中心，取旋转角等于∠BAC，把△ABC逆时针旋转，请用无刻度的直尺，画出旋转后的△AB'C'，保留作图痕迹，不要求证明；

（3）点P是BC边上任意一点，在（2）的旋转过程中，点P的对应点为P'，当线段CP'最短时，CP'的长度为　　．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(-1，0)，其部分图象如图所示，下列结论：① 4ac<b2；② 方程ax2＋bx＋c＝0的两个根分别是x1＝-1，x2＝3；③ 3a＋c>0；④当 y>0时，x的取值范围是-1<x<3；⑤ 当x<0时，y随x的增大而增大．其中正确的结论序号有_____________________．