
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=________
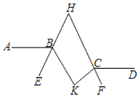
【答案】78°.
【解析】
分别过K、H作AB的平行线MN和RS,根据平行线的性质和角平分线的性质可用∠ABK和∠DCK分别表示出∠H和∠K,从而可找到∠H和∠K的关系,结合条件可求得∠K.
如图,分别过K、H作AB的平行线MN和RS,
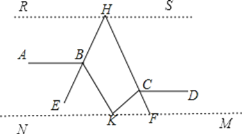
∵AB∥CD,
∴AB∥CD∥RS∥MN,
∴∠RHB=∠ABE=![]() ∠ABK,∠SHC=∠DCF=
∠ABK,∠SHC=∠DCF=![]() ∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,
∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,
∴∠BHC=180°-∠RHB-∠SHC=180°-![]() (∠ABK+∠DCK),
(∠ABK+∠DCK),
∠BKC=180°-∠NKB-∠MKC=180°-(180°-∠ABK)-(180°-∠DCK)=∠ABK+∠DCK-180°,
∴∠BKC=360°-2∠BHC-180°=180°-2∠BHC,
又∠BKC-∠BHC=27°,
∴∠BHC=∠BKC-27°,
∴∠BKC=180°-2(∠BKC-27°),
∴∠BKC=78°,
故答案为:78°.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用水,某市决定对居民用水收费实行“阶梯价”,即当每月用水量不超过15吨时(包括15吨),采用基本价收费;当每月用水量超过15吨时,超过部分每吨采用市场价收费.小兰家4、5月份的用水量及收费情况如下表:
月份 | 用水量(吨) | 水费(元) |
4 | 22 | 51 |
5 | 20 | 45 |
(1)求该市每吨水的基本价和市场价.
(2)设每月用水量为n吨,应缴水费为m元,请写出m与n之间的函数关系式.
(3)小兰家6月份的用水量为26吨,则她家要缴水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.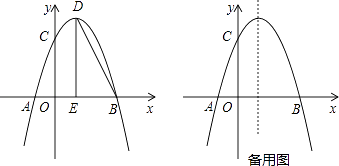
(Ⅰ)求抛物线的解析式及点D的坐标;
(Ⅱ)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(Ⅲ)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为正方形ABCD对角线的交点,点E,F分别在DA和CD的延长线上,且AE=DF,连接BE,AF,延长FA交BE于G.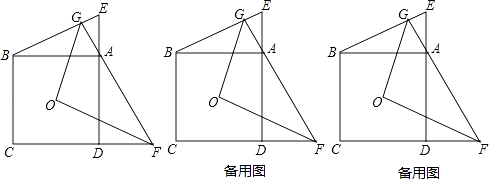
(1)试判断FG与BE的位置关系,并证明你的结论;
(2)连接OG,求∠OGF的度数;
(3)若AE= ![]() ,tan∠ABG=
,tan∠ABG= ![]() ,求OG的长.
,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
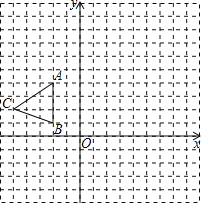
【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)写出△A1B1C1的面积;△A2B2C2的面积.(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
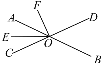
A. 95° B. 65°
C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(x,y),点A′(x′,y′),若x′=x+m,y′=y+n,即点A′(x+m,y+n),则表示点A到点A′的一个平移.例如:点A(x,y),点A′(x′,y′),若x′=x+1,y′=y-2,则表示点A向右平移1个单位长度,再向下平移2个单位长度得到点A′.
根据上述定义,探究下列问题:
(1)已知点A(x,y),A′(x-3,y),则线段AA′的长度是多少;
(2)已知点A(x,y),A′(x+2,y-1),则线段AA′的长度是多少;
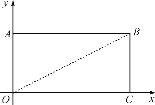
(3)长方形AOCB在平面直角坐标系中的位置如图所示,A(0,2),C(4,0),点A′(x′,y′),若x′=x+m,y′=y-2m(m均为正数),点A′(x′,y′)能否在△OCB的直角边上?若能,求m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF;
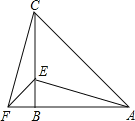
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AB=CE+BF;
(3)若∠CAE=30°,求∠ACF度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com