
 如图,直线y=2x与双曲线y=$\frac{2}{x}$在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
如图,直线y=2x与双曲线y=$\frac{2}{x}$在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )| A. | (2,0) | B. | (2,-1) | C. | (-2,1) | D. | (-1,-2) |
分析 通过解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$可得A(1,2),则AB=2,OB=1,再根据旋转的性质得AB=A′B′=2,OB=OB′=1,∠A′B′O=∠ABO=90°,∠BOB′=90°,所以点B′在y轴的正半轴上,A′B′⊥y轴,然后利用第二象限点的坐标特征写出A′点的坐标.
解答 解: 解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,则A(1,2),
解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,则A(1,2),
∵AB⊥x轴,
∴B(1,0),
∴AB=2,OB=1,
∵△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),如图,
∴AB=A′B′=2,OB=OB′=1,∠A′B′O=∠ABO=90°,∠BOB′=90°,
∴点B′在y轴的正半轴上,A′B′⊥y轴,
∴A′点的坐标为(-2,1).
故选C.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了旋转的性质.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:选择题
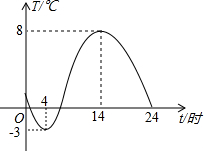 如图,是一台自动测温记录仪的图象,它反映了嵊州市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
如图,是一台自动测温记录仪的图象,它反映了嵊州市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )| A. | 凌晨4时气温最低为-3℃ | |
| B. | 从0时至14时,气温随时间增长而上升 | |
| C. | 14时气温最高为8℃ | |
| D. | 从14时至24时,气温随时间增长而下降 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠1=∠2,PC⊥OA,PD⊥OB,垂足分别为点C、D,则下列结论中错误的是( )
如图,∠1=∠2,PC⊥OA,PD⊥OB,垂足分别为点C、D,则下列结论中错误的是( )| A. | PD=OD | B. | PC=PD | C. | ∠DPO=∠CPO | D. | OD=OC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点落在点B′处.已知折痕EF=13,则AE的长等于$\frac{169}{24}$.
如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点落在点B′处.已知折痕EF=13,则AE的长等于$\frac{169}{24}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15.6 | B. | 19 | C. | 20 | D. | 22 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{69}$$>\sqrt{16}$ | B. | -$\sqrt{10}$>$\root{3}{-27}$ | C. | $\frac{\sqrt{7}-2}{2}<\frac{1}{2}$ | D. | $\sqrt{15}<2\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com