
 如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点落在点B′处.已知折痕EF=13,则AE的长等于$\frac{169}{24}$.
如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点落在点B′处.已知折痕EF=13,则AE的长等于$\frac{169}{24}$. 分析 过点F作FG⊥AD,垂足为G,连接AA′,在△GEF中,由勾股定理可求得EG=5,轴对称的性质可知AA′⊥EF,由同角的余角相等可证明∠EAH=∠GFE,从而可证明△ADA′≌△FGE,故此可知GE=DA′=5,最后在△EDA′利用勾股定理列方程求解即可.
解答 解:过点F作FG⊥AD,垂足为G,连接AA′.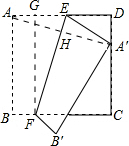
在Rt△EFG中,EG=$\sqrt{E{F}^{2}-F{G}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5.
∵轴对称的性质可知AA′⊥EF,
∴∠EAH+∠AEH=90°.
∵FG⊥AD,
∴∠GEF+∠EFG=90°.
∴∠DAA′=∠GFE.
在△GEF和△DA′A中,
$\left\{\begin{array}{l}{∠EGF=∠D=90°}\\{FG=AD}\\{∠DAA′=∠GFE}\end{array}\right.$,
∴△GEF≌△DA′A.
∴DA′=EG=5.
设AE=x,由翻折的性质可知EA′=x,则DE=12-x.
在Rt△EDA′中,由勾股定理得:EA′2=DE2+A′D2,即x2=(12-x)2+52.
解得:x=$\frac{169}{24}$.
故答案为:$\frac{169}{24}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用、全等三角形的性质和判定,证得△GEF≌△DA′A从而求得A′D=5是解题的关键.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=2x与双曲线y=$\frac{2}{x}$在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )
如图,直线y=2x与双曲线y=$\frac{2}{x}$在第一象限的交点为A,过点A作AB⊥x轴,垂足为B,将△ABO绕点O逆时针旋转90°,得到△A′B′O(点A对应点A′),则点A′的坐标是( )| A. | (2,0) | B. | (2,-1) | C. | (-2,1) | D. | (-1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$ | B. | $\sqrt{0}$ | C. | $\root{3}{-8}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC的外部作等腰三角形ACE和等腰三角形ABD,使AB=AD,AC=AE,∠DAB=∠CAE=45°,连接BE,CD.
如图,在△ABC的外部作等腰三角形ACE和等腰三角形ABD,使AB=AD,AC=AE,∠DAB=∠CAE=45°,连接BE,CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0)、(-3,1),AB=AC.
如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0)、(-3,1),AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com