
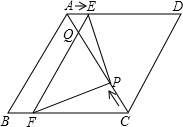
 如图,在?ABCD中,AB=6cm,AD=AC=5cm.点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF.若设运动时间为t(s)(0<t≤2.5).
如图,在?ABCD中,AB=6cm,AD=AC=5cm.点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF.若设运动时间为t(s)(0<t≤2.5).分析 (1)根据题意推出AP的长度,然后推出△APE∽△ACD,根据对应边成比例,即可推出t的值,推出点P、E分别为AC、AD的中点,即可推出EF的长度;
(2)作PG⊥EF于G,就可以而出EG=3,由AB∥EF就可以得出$\frac{AE}{AD}$=$\frac{EQ}{CD}$,就可以表示出EQ,近而表示出GQ和PQ,在Rt△PGQ中由勾股定理就可以表示出PG,根据三角形的面积公式就可以求出y与t的关系式.
(3)如图2,过C作CG⊥AB于G,由勾股定理得到CG=4,根据S△PEQ=$\frac{2}{25}$S△ABC,列方程即可得到结论;
(4)由(2)的全等三角形知:△AEP、△EPC的面积相等,因此五边形的面积可转化为△ABC的面积,所以五边形的面积是个定值;
解答 解:(1)∵AE=BF=CP=t,
∴AP=5-t,
在?ABCD中,AD=BC=AC=5,AB=EF=CD=6,
∵PE∥CD,
∴△APE∽△ACD,
∴$\frac{t}{5}$=$\frac{5-t}{5}$,
∴t=2.5,
∴当t=2.5时,PE∥CD;
(2)如图1,作PG⊥EF于G,
∴EG=$\frac{1}{2}$EF.
∵AE∥BF,AB∥EF,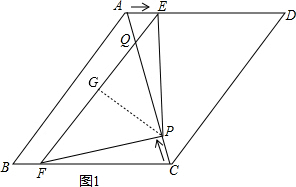
∴四边形ABFE是平行四边形,
∴AB=EF.
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴$\frac{AE}{AD}$=$\frac{EQ}{CD}$,
∴$\frac{t}{5}$=$\frac{EQ}{6}$,
∴EQ=$\frac{6}{5}$t,
∴GQ=3-$\frac{6}{5}$t.
∵CP=AQ=t,
∴PQ=5-2t,
在Rt△PGQ中,由勾股定理,得
PG=$\sqrt{(5-2t)^{2}-(3-\frac{6}{5}t)^{2}}$
=4-$\frac{8}{5}$t.
∵S△PQE=$\frac{1}{2}$EQ•PG,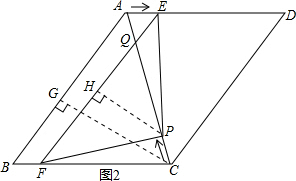
∴y=$\frac{1}{2}$×$\frac{6}{5}$t×(4-$\frac{8}{5}$t),
=-$\frac{24}{25}$t2+$\frac{12}{5}$t(0<t<2.5).
∴y与t之间的函数关系式为:y=-$\frac{24}{25}$t2+$\frac{12}{5}$t(0<t<2.5);
(3)如图2,过C作CG⊥AB于G,
在?ABCD中,AB=6cm,AD=AC=5cm,
∴BC=AD=AC=5,
∴BG=$\frac{1}{2}$AB=3,
∴CG=4,
∵S△PEQ=$\frac{2}{25}$S△ABC,
∴-$\frac{24}{25}$t2+$\frac{12}{5}$t=$\frac{2}{25}$×$\frac{1}{2}×6×4$,
∴t=2,或t=$\frac{1}{2}$,
∴当t=2或$\frac{1}{2}$时,S△PEQ=$\frac{2}{25}$S△ABC;
(4)是定值,为12.
理由:由(2)的全等三角形知:S△AEP=S△PCF,即S五边形BFPEA=S△ABC;
过C作CG⊥AB于G,
等腰△ACB中,AG=BG=3,AC=BC=5,则CG=4;
∴S五边形BFPEA=S△ABC=$\frac{1}{2}$×6×4=12.
点评 本题考查了平行四边形的性质的运用,等腰三角形的判定及性质的运用,勾股定理的运用,平行线分线段成比例定理的运用,三角形的面积公式的运用,解答时运用相似表示出EQ的值和运用勾股定理表示PG的值是解答本题的难点和关键.


科目:初中数学 来源: 题型:选择题
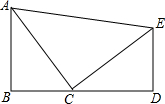 如图,AB⊥BD,ED⊥BD于D,AB=CD,AC=CE,下列结论:(1)BC=DE;(2)AC⊥CE;(3)∠CAE=45°,其中正确的有( )
如图,AB⊥BD,ED⊥BD于D,AB=CD,AC=CE,下列结论:(1)BC=DE;(2)AC⊥CE;(3)∠CAE=45°,其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
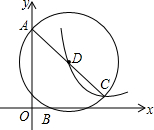 如图,平面直角坐标系中,已知A(0,3),B(1,0),点C在第一象限,⊙D经过点A、B、C三点,AC是⊙O的直径,双曲线y=$\frac{k}{x}$(x>0)经过D、C两点,则k的值是4.
如图,平面直角坐标系中,已知A(0,3),B(1,0),点C在第一象限,⊙D经过点A、B、C三点,AC是⊙O的直径,双曲线y=$\frac{k}{x}$(x>0)经过D、C两点,则k的值是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校综合实践活动小组与5月20日(中国学生营养日)开展快餐营养情况调查活动,他们在互联网查获的食品安全监督部门的一份快餐信息如图所示,请根据此信息,解答下列问题:
某校综合实践活动小组与5月20日(中国学生营养日)开展快餐营养情况调查活动,他们在互联网查获的食品安全监督部门的一份快餐信息如图所示,请根据此信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
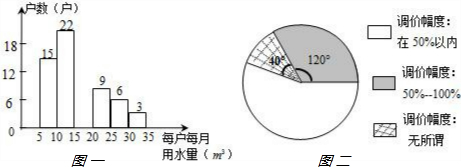
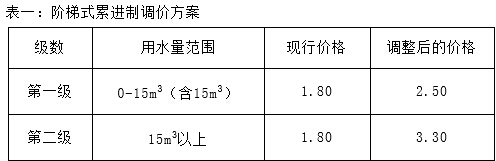
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
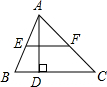 如图,已知在△ABC中,AD⊥BC,垂足为点D,若AD=$\frac{1}{2}$BC,EF为中位线,那么以EF为直径的圆与直线BC有怎样的位置关系?请说明理由.
如图,已知在△ABC中,AD⊥BC,垂足为点D,若AD=$\frac{1}{2}$BC,EF为中位线,那么以EF为直径的圆与直线BC有怎样的位置关系?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com