
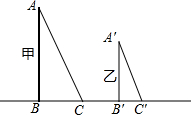
 同一时刻,不同高度的物体的影子的长短不相同,物高与影长之间存在“物高A:影长A=物高B:影长B(请证明此结论)
同一时刻,不同高度的物体的影子的长短不相同,物高与影长之间存在“物高A:影长A=物高B:影长B(请证明此结论) 分析 如图,物体AB的影长为BC,同一时物体A′B′的影长为B′C′,先证明△ACB∽△A′C′B′得到$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$,然后利用比例性质得到$\frac{AB}{BC}$=$\frac{A′B′}{B′C′}$,所以“物高A:影长A=物高B:影长B.
解答 证明:如图,物体AB的影长为BC,同一时刻 物体A′B′的影长为B′C′,
物体A′B′的影长为B′C′,
∵AB⊥BC,A′B′⊥B′C′,
∴∠ABC=∠A′B′C′=90°,
∵AC∥A′C′,
∴∠ACB=∠A′C′B′,
∴△ACB∽△A′C′B′,
∴$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$,
即$\frac{AB}{BC}$=$\frac{A′B′}{B′C′}$,
所以“物高A:影长A=物高B:影长B.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com