
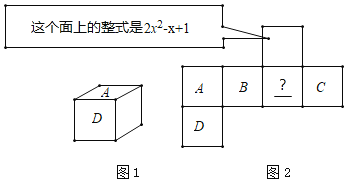
【题目】把正方体(图1)沿着某些棱边剪开,就可以得到正方体的表面展开图,如图2.在图1正方体中,每个面上都写了一个含有字母x的整式,相对两个面上的整式之和都等于4x﹣7,且A+D=0,(说明:A、B、C、D都表示含有字母x的整式)请回答下面问题:
(1)把图1正方体沿着某些棱边剪开得到它的表面展开图2,要剪开 条棱边;
(2)整式B+C= ;
(3)计算图2中“D”和“?”所表示的整式(要写出计算过程).
【答案】(1)7;(2)4x﹣7;(3)﹣2x2+9x﹣15.
【解析】
(1)根据表面展开图即可得出要剪开几条棱边;
(2)根据相对两个面上的整式之和都等于4x﹣7即可求解;
(3)根据相对两个面上的整式之和都等于4x﹣7可求D,再根据A+D=0可求A,再根据相对两个面上的整式之和都等于4x﹣7可求“?”.
解:(1)把图1正方体沿着某些棱边剪开得到它的表面展开图2,要剪开7条棱边;
故答案为:7;
(2)整式B+C=4x﹣7;
故答案为:4x﹣7;
(3)D=4x﹣7﹣(2x2﹣x+1)=4x﹣7﹣2x2+x﹣1=﹣2x2+5x﹣8;
A=﹣D=2x2﹣5x+8;
“?”=4x﹣7﹣(2x2﹣5x+8)=4x﹣7﹣2x2+5x﹣8=﹣2x2+9x﹣15.


科目:初中数学 来源: 题型:
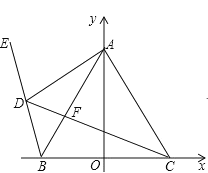
【题目】如图,已知 B 1, 0 , C 1, 0 , A 为 y 轴正半轴上一点, AB AC ,点 D 为第二象限一动点,E 在 BD 的延长线上, CD 交 AB 于 F ,且BDC BAC .
(1)求证: ABD ACD ;
(2)求证: AD 平分CDE ;
(3)若在 D 点运动的过程中,始终有 DC DA DB ,在此过程中,BAC 的度数是否变化?如果变化,请说明理由;如果不变,请求出BAC 的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某路公交车从起点站出发依次经过A、B、C站到达终点站,各站上、下乘客人数如下表所示(记上车人数为正,下车人数为负).
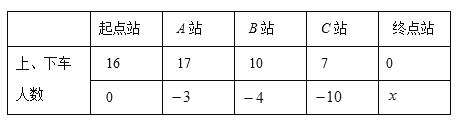
(1)表格中![]() 的值是 ;
的值是 ;
(2)若此公交车采用一票制,即每位上车乘客无论哪站下车,车票都是2元,问该车这次出车共收入多少元?请列式计算.
(3)通过列式计算,公交车行驶在哪两站之间时车上的乘客最多?最多乘客人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:

①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.
考点:三角形综合题.
【题型】填空题
【结束】
19
【题目】先化简,再求值:(a+1-![]() )÷(
)÷(![]() ),其中a=2+
),其中a=2+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F。

(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,BE=2,求∠F的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
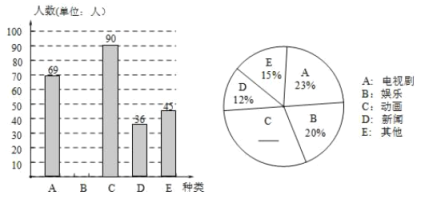
(1)本次调查的学生人数为__________,娱乐节目在扇形统计图中所占圆心角的度数是__________度.
(2)请将条形统计图补充完整:
(3)若该中学有2000名学生,请估计该校喜爱动画节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图l所示,给定线段MN及其垂直平分线上一点P。若以点P为圆心,PM为半径的优弧(或半圆弧)MN上存在三个点可以作为一个等边三角形的顶点,则称点P为线段MN的“三足点”,特别的,若这样的等边三角形只存在一个,则称点P为线段MN的“强三足点”。
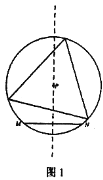
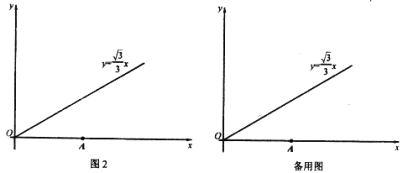
问题:如图2所示,平面直角坐标系xOy中,点A的坐标为(2![]() ,0),点B在射线y=
,0),点B在射线y=![]() x(x≥0)上。
x(x≥0)上。
(1)在点C(![]() ,0),D(
,0),D(![]() ,1),E(
,1),E(![]() ,-2)中,可以成为线段OA的“三足点”的是__________.
,-2)中,可以成为线段OA的“三足点”的是__________.
(2)若第一象限内存在一点Q既是线段OA的“三足点”,又是线段OB的“强三足点”,求点B的坐标。
(3)在(2)的条件下,以点A为圆心,AB为半径作圆,假设该圆与x轴交点中右侧一个为H,圆上一动点K从H出发,绕A顺时针旋转180°后停止,设点K出发后转过的角度为![]() (0°<
(0°< ![]() ≤180°),若线段OB与AK不存在公共“三足点”,请直接写出
≤180°),若线段OB与AK不存在公共“三足点”,请直接写出![]() 的取值范围是_______________。
的取值范围是_______________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两辆汽车从相距84 km的两地同时出发相向而行,甲车的速度比乙车的速度快20 km/h,半小时后两车相遇.
(1)求乙车的速度是每小时多少千米?
(2)甲车的速度是_______ km/h;
(3)两车相遇时,甲车比乙车多行驶________千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com