
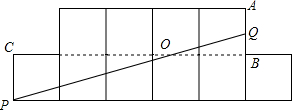
 如图是由10个边长为1的小正方形组成的图形,点P在一正方形的顶点,点Q在边AB上,PQ与BC交于点0,若PQ恰将这图形的面积平分,则$\frac{QO}{OP}$的值是$\frac{3}{5}$.
如图是由10个边长为1的小正方形组成的图形,点P在一正方形的顶点,点Q在边AB上,PQ与BC交于点0,若PQ恰将这图形的面积平分,则$\frac{QO}{OP}$的值是$\frac{3}{5}$. 分析 首先设QB=x,根据题意得到PQ下面的部分的面积为:S△+S正方形=$\frac{1}{2}$×5×(1+x)+1=5,解方程即可求得QB的长,由△POC∽△QOB对应边成比例可得结果.
解答 解:设QB=x,
∵PQ恰将这个图形平分成两个面积相等的部分,
∴PQ下面的部分的面积为:S△+S正方形=$\frac{1}{2}$×5×(1+x)+1=5,
解得:x=$\frac{3}{5}$,
∴QB=$\frac{3}{5}$,
∵△POC∽△QOB,
∴$\frac{QO}{OP}=\frac{QB}{PC}=\frac{\frac{3}{5}}{1}=\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 此题考查了不规则图形的面积的求解方法及相似三角形的判定与性质,要注意仔细识图是基础,注意将原图形分割求解是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 明天太阳从西方升起 | |
| B. | 掷一枚硬币,正面朝上 | |
| C. | 任意一个三角形,它的内角和等于180° | |
| D. | 打开电视机,正在播放“安徽新闻” |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -5 | -2 | 1 | 4 | 7 | 10 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
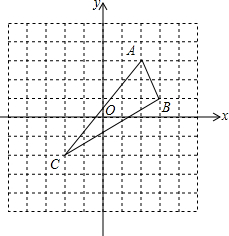 如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出E、F的坐标.
如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出E、F的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com