
����Ŀ�������龳��
����֪����������ƽ���߱�������ֱ�����أ�ͬλ����ȣ��ڴ�����ȣ�ͬ���ڽǻ�������������ijЩ̽����������ͨ��������ƽ������������ת�������ã�
��֪���ǰ�![]() �У�
��![]() ��������
��������![]() ��
��![]() ��
��
�����̽��
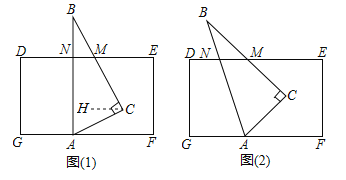
��1����ͼ��1�����������ǰ�![]() �Ķ���
�Ķ���![]() ���ڳ����εı�
���ڳ����εı�![]() �ϣ�
�ϣ�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �Ķ�����
�Ķ�����
����![]() ��
��![]() ������
������![]() ���Ӷ���
���Ӷ���![]() ���Ӷ��������
���Ӷ��������![]() �Ķ�����
�Ķ�����
�ɷ����ã�����ֱ��д����![]() �Ķ���Ϊ____________��
�Ķ���Ϊ____________��![]() �Ķ���Ϊ___________��
�Ķ���Ϊ___________��
�����̽��
��2���������ǰ�![]() ��ͼ��2����ʾ��ʽ�ڷţ�
��ͼ��2����ʾ��ʽ�ڷţ�![]() ��
��![]() ����ֱ�����������д��
����ֱ�����������д��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
���𰸡���1��30����60������2����CAF+��EMC=90�������ɼ�����
��������
��1�����á�CAF=��BAF-��BAC�����CAF���������EMC����ת������MCH������
��2������C��CH��GF���õ�CH��DE����CAF���EMCת������ACH�͡�MCH�У��Ӷ����֡�CAF����EMC���ACB��������ϵ��
��1������C��CH��GF������CH��DE��
���ԡ�CAF=��HCA����EMC=��MCH��
�ߡ�BAF=90����
���CAF=90��-60��=30����
��MCH=90��-��HCA=60����
���EMC=60����
�ʴ�Ϊ30����60����
��2����CAF+��EMC=90�����������£�
����C��CH��GF�����CAF=��ACH��
��DE��GF��CH��GF��
��CH��DE��
���EMC=��HCM��
���EMC+��CAF=��MCH+��ACH=��ACB=90����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽص��ҵ���������·��һ����ȫ��600km����ͨ��·����һ����ȫ��480km�ĸ��ٹ�·��ij�ͳ��ڸ��ٹ�·����ʻ��ƽ���ٶȱ�����ͨ��·�Ͽ�45![]() /
/![]() ���ɸ��ٹ�·�Ӽص��ҵ������ʱ��������ͨ��·�Ӽص��ҵ�����ʱ���һ�룬��ÿͳ��ɸ��ٹ�·�Ӽص��ҵ������ʱ�䣮
���ɸ��ٹ�·�Ӽص��ҵ������ʱ��������ͨ��·�Ӽص��ҵ�����ʱ���һ�룬��ÿͳ��ɸ��ٹ�·�Ӽص��ҵ������ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=Rt�ϣ���BCΪֱ���ġ�O��AB�ڵ�D������DE��AC�ڵ�E.
��1����֤����A=��ADE��
��2����AD=16��DE=10����BC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
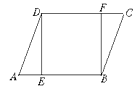
����Ŀ����ͼ����ƽ���ı�ABCD�У�E��F�ֱ���AB��DC�ϵĵ㣬��AE=CF��
��1����֤����ADE�ա�CBF��
��2�� ����DEB=90��ʱ����˵���ı���DEBFΪ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڽǷֱ������ǶԽǵ�һ����ı��ν�����Խ��ı��Σ�
��1����ͼ1���ڰ�Խ��ı���ABCD�У���B�� ![]() ��D����C��
��D����C�� ![]() ��A�����B���C�Ķ���֮�ͣ�
��A�����B���C�Ķ���֮�ͣ�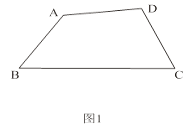
��2����ͼ2����ǡ�ABC�ڽ��ڡ�O������AB�ϴ���һ��D��ʹ��BD��BO����OBA��ƽ���߽�OA�ڵ�E������DE���ӳ���AC�ڵ�F����AFE��2��EAF��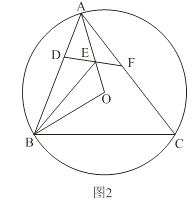
��֤���ı���DBCF�ǰ�Խ��ı��Σ�
��3����ͼ3���ڣ�2���������£�����D��DG��OB�ڵ�H����BC�ڵ�G����DH��BGʱ�����BGH���ABC�����֮�ȣ�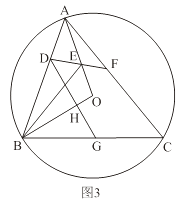
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�Rt��AOB������ֱ�DZ�OA��OB�ֱ���x���y���ϣ�OA=3��OB=4���ѡ�AOB�Ƶ�A˳ʱ����ת120�㣬�õ���ADC����OB�ϵ�һ��M��ת��Ķ�Ӧ��ΪM�䣬��AM��+DMȡ����Сֵʱ����M������Ϊ�� ��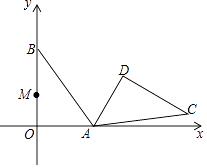
A.��0�� ![]() ��
��
B.��0�� ![]() ��
��
C.��0�� ![]() ��
��
D.��0��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1������ ![]() ��
�� ![]() ����
���� ![]() +
+ ![]()
��2�����㣺����3����2+ ![]() ��|1��2
��|1��2 ![]() |����
|���� ![]() ��3��0 ��
��3��0 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ھ���![]() �У�AB=30cm��BC=60cm����
�У�AB=30cm��BC=60cm����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ·�����
·�����![]() �����˶��������
�����˶��������![]() ��ֹͣ����
��ֹͣ����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ·�����
·�����![]() �����˶��������
�����˶��������![]() ��ֹͣ������
��ֹͣ������![]() ͬʱ���������˶������У�
ͬʱ���������˶������У�![]() ��ͣ����
��ͣ����![]() ��ͼ����
��ͼ����![]() ����������
����������![]() ������·��S(cm)��ʱ��
������·��S(cm)��ʱ��![]() (s)֮��IJ��ֺ�����ϵͼ����
(s)֮��IJ��ֺ�����ϵͼ����
��1��P��Q������˶��ٶȼ�P��C���ʱ�䣻
��2����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��y=y1+y2 �� y1��x����������y2��x�ɷ���������x=2ʱ��y=��4����x=��1ʱ��y=5����y��x�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com